 |
NO ME SALEN
PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC
(Movimiento uniformemente variado)
|
|

|
| |

|
1) ¿En qué distancia se detendrá, al frenar, una moto que se mueve a 120 km/h, si esa misma moto, moviéndose a 60 km/h, se detiene en 50 m? Considere que la fuerza de frenado es constante y la misma en ambos casos.
a) 50 m b) 100 m
c) 150 m d) 200 m
e) faltan datos f) ninguna de las anteriores |
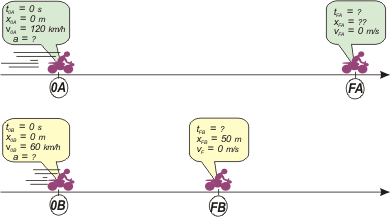
Este ejercicio contiene un dato que para poder interpretarlo hay que tener ciertos conocimientos de dinámica, y es el siguiente: el hecho de que la fuerza de frenado sea la misma en ambos casos se traduce en que en ambos movimientos la aceleración es la misma. Advertidos de esto voy a empezar con un esquema que en este caso en particular serán dos esquemas, ya que se trata de dos movimientos diferentes e independientes. Acá van:
| | |
 |
|
|
Notarás que llamé A al primer movimiento, aquel sobre el cual nos hacen una pregunta; y B al segundo, el que nos ofrecen como dato. Por eso utilicé un doble subíndice, con una A a todo lo que pertenece al primer movimiento y una B a lo del segundo. Excepto para la aceleración, ya que aA = aB = a. Volvé a mirarlo con detenimiento.
Ahora vamos a armar las ecuaciones horarias que describen los movimientos. Tenés que tener los modelos a mano:
x = xo + vo ( t – to ) + ½ a ( t – to )2
v = vo + a ( t – to )
y reemplazar las constantes del modelo (las que te escribí en verde) por las constantes de los movimientos y que están todas en los globitos iniciales de cada uno. Antes de usar ningún dato voy a expresarlos a todos en las mismas unidades. |
|
|
| |
x = 33,33 m/s t + ½ a t ² |
|
Estas son las ecuaciones que describen todo el movimiento de la moto en la situación A |
| v = 33,33 m/s + a t |
|
| |
x = 16,67 m/s t + ½ a t ² |
|
Estas son las ecuaciones que describen todo el movimiento de la moto en la situación B |
| |
v = 16,67 m/s + a t |
|
|
|
|
| Ahora que tengo armadas las ecuaciones que describen los movimientos, vamos a usarlas, es decir, les voy a pedir que hablen de los puntos en los que tengo un interés especial, o sea, los instantes finales de cada uno, cuando se detienen. |
|
|
| |
xFA = 33,33 m/s tFA + ½ a tFA² |
[1] |
caso A cuando se detiene |
| 0 m/s = 33,33 m/s + a tFA |
[2] |
| 50 m = 16,67 m/s tFB + ½ a tFB² |
[3] |
caso B cuando se detiene |
| 0 m/s = 16,67 m/s + a tFB |
[4] |
|
|
|
Otra vez sopa. Cuatro ecuaciones y cuatro incógnitas. A partir de aquí se trata de una cuestión algebraica, no física.
De la ecuación [4] despejo y calculo tFB
|
|
|
|
|
|
| eso lo meto en la ecuación [3] |
|
|
| 50 m = |
|
–( 16,67 m/s)² |
+ |
½ ( 16,67 m/s)² |
|
|
|
|
| a |
a |
|
|
|
| 50 m = |
|
– ½ ( 16,67 m/s)² |
|
|
|
| a |
|
|
|
a = – 2,77 m/s²
vuelvo a la [4]
tFB = 6 s
ahora me voy a la [2]
tFA = 12 s
y por último llego a la ecuación [1] |
|
|
| |
|
|
El ejercicio no nos pide los gráficos, pero es una obligación moral hacerlos y, como siempre, vas a ver que podemos sacarles un buen provecho. |
|
|
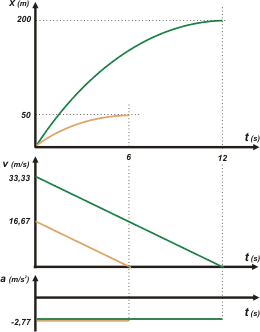 |
Usé los mismos colores que en el esquema. Fijate la inclinación de las curvas de posición en los instantes finales.
Mirá ahora las gráficas de velocidad... parecen paralelas, ¿no es cierto? |
| |
| Desafío. Para hacer mentalmente: decime dónde se detendría la moto si marchase a 180 km/h. |
|
|
 |
|
|
| Algunos derechos reservados.
Se prohibe estrictamente leer este ejercicio resuelto por encima, hay que leerlo despacio y con atención. Las penalizaciones a esta infracción son severas. Se permite su reproducción citando la fuente. Última actualización sep-07. Buenos Aires, Argentina. |
|
|
|

