 |
NO ME SALEN
PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC
(Movimiento uniformemente variado)
|
|

|
| |

|
14) Un cuerpo cae libremente, partiendo del reposo, y emplea 4 segundos en recorrer la
primera mitad de su desplazamiento.
a) ¿Cuál es el desplazamiento total?
b) ¿Con qué velocidad pasa por la mitad de su recorrido?
c) ¿En qué instante y con qué velocidad termina el recorrido? |
Este ejercicio era un poco tontito, así que yo le agregué la última pregunta que lo hace más interesante.
| | |
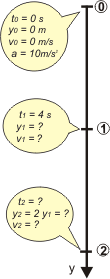 |
Voy a empezar con un esquema que me va a permitir organizar toda la información y, de paso, ponerle nombre adecuado a todos los datos.
Elegí un SR que apunta hacia abajo, pero bien podría haber elegido el contrario. Sólo lo hice para que no llores.
Ahora vamos a armar las ecuaciones horarias que describen el movimiento. Vas a ver qué facil. Tenés que tener los modelos a mano
y = yo + vo ( t – to ) + ½ g ( t – to )²
v = vo + g ( t – to )
y reemplazar las constantes del modelo (las que te escribí en verde) por las constantes del movimiento (en general se eligen las iniciales) y que están todas en el globito de arriba (qué casualidad). Así quedan:
|
|
|
| cuando armás un esquema al mismo tiempo estás eligiendo un Sistema de Referencia |
|
| |
y = 5 m/s² t² |
|
Estas son las ecuaciones que describen todo el movimiento, son las que todos se saltean: las ignoran. Y son lo más importante de la física del ejercicio. |
| v = 10 m/s² t |
|
|
|
|
| Ahora que tengo armadas las ecuaciones que describen el movimiento, vamos a usarlas, es decir, les voy a pedir que hablen de los puntos en los que tengo un interés especial: el 1 y el 2. |
|
|
 |
y1 = 5 m/s² 16 s² |
|
[1] |
|
| v1 = 10 m/s² 4 s |
|
[2] |
|
| y2 = 2 y1 = 5 m/s² t2² |
|
[3] |
|
| v2 = 10 m/s² t2 |
|
[4] |
|
|
|
|
Inevitablemente llego a un sistema de tantas ecuaciones como incógnitas (en este caso 5 y 5, ya que la expresión [3] tiene dos ecuaciones metidas) y sólo resta resolverlo. Fijate que las incógnitas te las pinté de azul. No son las variables, son las incógnitas, tan constantes como cualquier constante. ¿Entendés?
A partir de aquí se trata de una cuestión algebraica, no física... y bastante sencilla, por cierto. Yo te ayudo:
Con la ecuación [1] calculo y1 |
|
|
| |
|
|
Sabido y1, es trivial conocer y2 |
|
|
|
|
|
| Con la ecuación [2] calculo v1 |
|
|
|
|
|
| De la ecuación [3] y conociendo y2, despejo t2 y lo calculo |
|
|
|
|
|
| Finalmente, con ese dato averiguado voy a la última ecuación y obtengo v2 |
|
|
|
|
|
Ahora, como siempre y en tándem, te voy a hacer los gráficos. |
|
|
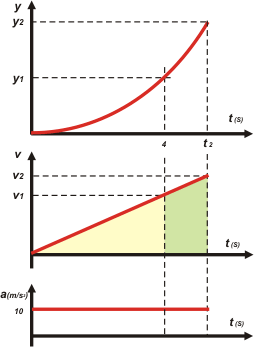 |
El orden del tándem x, v, a, no es caprichoso ni arbitrario... tiene su lógica, y el hecho de que los tres se confeccionen con la misma escala de tiempo permite acceder a toda la información cinemática de un solo golpe de vista.
Fijate que se podría haber hecho de entrada y sin conocer los resultados. Lo que importa es lo cualitativo, en este caso: que la distancia entre y1 e y2 sea igual a la de y1 y 0; que las curvas son parábola, recta oblicua y recta horizontal; que la parábola arranca con una inclinación nula, que la relación entre los instantes y las velocidades nos parezca razonable... etcétera. |
| Animate a decirme sin hacer ningún cálculo que no sea mentalmente cuál de las dos áreas que coloreé es mayor. Y si no te sale, calculalo... y avivate. |
| Desafío: resolvé el mismo problema pero eligiendo un sistema de referencia con sentido opuesto al que elegimos acá. |
|
|
 |
Algunos derechos reservados.
Se permite su reproducción citando la fuente.
Última actualización mar-08. Buenos Aires, Argentina. |
|
| |
|

