 |
NO ME SALEN
PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC
(Movimiento uniformemente variado)
|
|

|
| |

|
13) Un objeto cae partiendo del reposo desde una altura de 25 m respecto del piso.
a) ¿Cuánto tiempo tarda en llegar al piso?
b) ¿A qué altura del piso se hallará a los 2 s de la partida?
c) ¿Qué velocidad tendrá en ese momento?
d) Grafique la posición y la velocidad desde que parte hasta que llega al piso.
e) ¿Con qué velocidad, como mínimo, debería ser lanzado desde el piso hacia
arriba para llegar otra vez hasta una altura de 25 m? |
Voy a empezar con un esquema que me va a permitir organizar toda la información y, de paso, ponerle nombre adecuado a todos los datos.
| | |
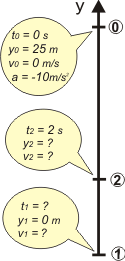 |
Elegí un SR que apunta hacia arriba, pero bien podría haber elegido el contrario. Sólo lo hice para hacerte enojar. Y para mostrarte que la elección del SR es independiente de lo que haga el móvil y sólo depende de tu inspiración, tu capricho. El ejercicio que sigue en muuuy parecido a éste, y está resuelto con un SR contrario a éste.
Ahora vamos a armar las ecuaciones horarias que describen el movimiento. Vas a ver qué facil. Tenés que tener los modelos a mano:
y = yo + vo ( t – to ) + ½ g ( t – to )²
v = vo + g ( t – to )
y reemplazar las constantes del modelo (las que te escribí en verde) por las constantes del movimiento (en general se eligen las iniciales) y que están todas en el globito de arriba (qué casualidad). Así quedan: |
|
|
| cuando armás un esquema al mismo tiempo estás eligiendo un Sistema de Referencia |
|
| |
y = 25 m – 5 m/s² t² |
|
Estas son las ecuaciones que describen todo el movimiento, son las que todos se saltean: las ignoran. Y son lo más importante de la física del problema |
| v = – 10 m/s² t |
|
|
|
|
| Ahora que tengo armadas las ecuaciones que describen el movimiento, vamos a usarlas, es decir, les voy a pedir que hablen de los puntos en los que tengo un interés especial: el 1 y el 2. |
|
|
 |
0 m = 25 m – 5 m/s² t1² |
|
[1] |
|
| v2 = – 10 m/s² . 2 s |
|
[2] |
|
| y2 = 25 m – 5 m/s² . 4 s² |
|
[3] |
|
|
|
|
Inevitablemente llego a un sistema de tantas ecuaciones como incógnitas (en este caso 3 y 3), y sólo resta resolverlo. Fijate que las incógnitas te las pinté de azul. No son las variables, son las incógnitas, tan constantes como cualquier constante. ¿Entendés?
A partir de aquí se trata de una cuestión algebraica, no física... y bastante sencilla, por cierto. Yo te ayudo:
Con la ecuación [1] calculo t1 |
|
|
| |
|
|
Con la ecuación [2] calculo v2 |
|
|
|
|
|
| Y con la ecuación [3] calculo y2 |
|
|
|
|
|
Ahora, como siempre y en tándem, te voy a hacer los gráficos. |
|
|
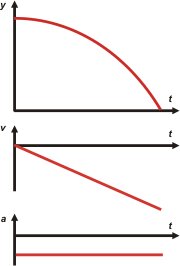 |
El orden del tándem x, v, a, no es caprichoso ni arbitrario... tiene su lógica, y el hecho de que los tres se confeccionen con la misma escala de tiempo permite acceder a toda la información cinemática de un solo golpe de vista.
Desafío: resolvé el mismo problema pero eligiendo un sistema de referencia con sentido opuesto al que elegimos acá. |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-08. Buenos Aires, Argentina. |
|
|
|
 |
| |
|

