 |
NO ME SALEN
PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC
(Movimiento uniformemente variado)
|
|

|
| |

|
11) Un subterráneo ingresa a una estación a 36 km/h. Debe detenerse en 10 segundos.
a) ¿Cuál debe ser su aceleración de frenado (supuestamente constante)?
b) ¿Qué distancia recorre el subte en los cinco primeros segundos, contados desde que entra a la estación?
c) ¿Qué velocidad tendrá el subte un segundo antes de detenerse? |
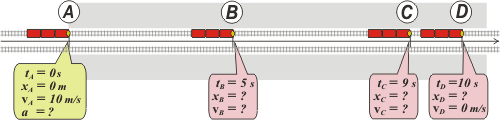
Prestale mucha atención a este esquema que me llevó un rato largo hacerlo.
| | |
 |
|
|
Habrás visto que transformé los 36 km/h en 10 m/s, su equivalente. (¿Ya aprendiste a hacer pasajes de unidades?). Ahora armo las ecuaciones horarias que describen el movimiento. Vas a ver qué facil. Tengo los modelos a la vista:
x = xo + vo ( t – to ) + ½ a ( t – to )2
v = vo + a ( t – to )
y en ellos reemplazamos las constantes del modelo (las que te escribí en verde) por las constantes del movimiento (en general se eligen las iniciales) y que están todas en el globito verde (qué casualidad). |
|
|
| |
x = 10 m/s t + ½ a t ² |
|
Estas son las ecuaciones que describen todo el fenómeno, son las que todos se saltean: las ignoran. Y son lo más importante de la física del problema |
| v = 10 m/s + a t |
|
|
|
|
| Ahora que tengo armadas las ecuaciones que describen el movimiento, vamos a usarlas, es decir, les voy a pedir que hablen del punto en el que tengo un interés especial: el B, el C y el D. |
|
|
 |
xB = 10 m/s 5 s + ½ a 25 s ² |
|
[1] |
acá hablan de B |
| vB = 10 m/s + a 5 s |
|
[2] |
| xC = 10 m/s 9 s + ½ a 81 s ² |
|
[3] |
acá hablan de C |
| vC = 10 m/s + a 9 s |
|
[4] |
| xD = 10 m/s 10 s + ½ a 100 s ² |
|
[5] |
acá hablan de D |
| 0 m/s = 10 m/s + a 10 s |
|
[6] |
|
|
|
Inevitablemente llego a un sistema de tantas ecuaciones como incógnitas (en este caso 6 y 6) y sólo resta resolverlo. A partir de aquí se trata de una cuestión algebraica, no física... y bastante sencilla, por cierto. Yo te ayudo:
De la ecuación [6] despejo y calculo a
–10 m/s = a 10 s
|
|
|
| |
|
|
Ahora con ese dato voy a cada una de las otras ecuaciones y obtengo las incógnitas que faltan (algunas de ellas el enunciado ni las pide, aunque podría). |
|
|
| |
|
|
vB = 5 m/s
xC = 49,5 m
|
|
|
|
|
|
xD = 50 m
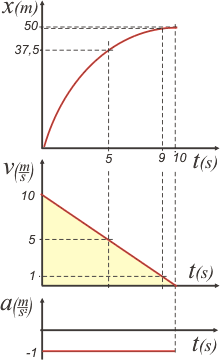
Tampoco nos piden los gráficos, pero... hay que hacerlos. |
|
|
 |

|
Los gráficos te permiten entender mejor esos números pelados de los resultados. Ahora queda claro por qué la posición un segundo antes de detenerse era tan próxima a la de detención.
El área sombreada vale 50 m, como habrás notado. |
| Desafío: resolvé el mismo problema pero eligiendo un sistema de referencia con sentido opuesto al que elegimos acá, y con una posición inicial (ingreso a la estación) de 120 m. |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización sep-07. Buenos Aires, Argentina. |
|
|
 |
|
|
|
| |
|

