 |
NO ME SALEN
PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC
(Movimiento uniformemente variado)
|
|

|
| |

|
9) Un móvil realiza un movimiento rectilíneo uniformemente variado, experimentando un desplazamiento de 32 m en un intervalo de tiempo de 4 segundos. Si la velocidad inicial es de 10 m/s, calcular la aceleración a que está sometido. |
Voy a empezar con un esquema que me va a permitir organizar toda la información y, de paso, ponerle nombre adecuado a todos los datos.
| | |
 |
|
| cuando armás un esquema al mismo tiempo estás eligiendo un Sistema de Referencia |
|
Ahora vamos a armar las ecuaciones horarias que describen el movimiento. Vas a ver qué facil. Tenés que tener los modelos a mano:
x = xo + vo ( t – to ) + ½ a ( t – to )2
v = vo + a ( t – to )
y reemplazar las constantes del modelo (las que te escribí en verde) por las constantes del movimiento (que en general se eligen las iniciales) y que están todas en el globito verde (qué casualidad). |
|
|
| |
x = 10 m/s t + ½ a t ² |
|
Estas son las ecuaciones que describen todo el fenómeno, son las que todos se saltean: las ignoran. Y son lo más importante de la física del problema |
| v = 10 m/s + a t |
|
|
|
|
| Ahora que tengo armadas las ecuaciones que describen el movimiento, vamos a usarlas, es decir, les voy a pedir que hablen del punto en el que tengo un interés especial: el 1. |
|
|
 |
32 m = 10 m/s 4 s + ½ a 16 s ² |
|
[1] |
|
| v1 = 10 m/s + a 4 s |
|
[2] |
|
|
|
|
Inevitablemente llego a un sistema de tantas ecuaciones como incógnitas (en este caso 2 y 2) y sólo resta resolverlo. A partir de aquí se trata de una cuestión algebraica, no física... y bastante sencilla, por cierto. Yo te ayudo:
De la ecuación [1] despejo y calculo a
32 m = 40 m + a 8 s²
– 8 m = a 8 s ²
|
|
|
| |
|
|
Es cierto que el enunciado no te pregunta cuánto vale la velocidad en ese instante... pero debería hacerlo. Yo te lo voy a calcular. Con ese valor de a, me voy a la ecuación [2] y nos queda:
v1 = 6 m/s
Tampoco nos piden los gráficos, pero es una obligación moral hacerlos. Como siempre... en tándem. |
|
|
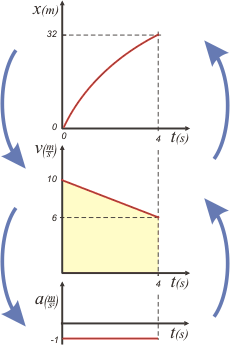 |
El orden del tándem x, v, a, no es caprichoso ni arbitrario... tiene su lógica: la función de la velocidad puede obtenerse derivando la de posición; y la de aceleración derivando la de velocidad (o, si querés: derivando dos veces la de posición).
A la inversa puedo regresar por el camino analítico integrando las funciones. |
| Esto no es sólo una disquisición matemática: tiene su lado práctico. Por ejemplo: integración tiene un correlato gráfico consistente en calcular áreas. Si hallamos el área encerrada bajo la curva de velocidad, obtenemos el desplazamiento correspondiente en el mismo intervalo de tiempo. |
| Desafío: resolvé el mismo problema pero eligiendo un sistema de referencia con sentido opuesto al que elegimos acá. |
|
|
 |
|
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización ago-07. Buenos Aires, Argentina. |
|
|
|

