NO ME SALEN
PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC
(Movimiento uniforme)
|
|

|
| |

|
6) Un corredor recorre 500 metros llanos en 80 segundos, a velocidad que puede
considerarse constante durante cada tramo. Al llegar al extremo del recorrido se detiene
durante diez segundos y retorna por el mismo camino en 100 segundos.
a) ¿Cuánto vale la velocidad a la ida? ¿Cuánto vale la velocidad a la vuelta?
b) Grafique la posición del corredor desde que sale hasta que vuelve.
c) ¿Dónde se hallará el corredor a los 40, a los 85 y a los 125 segundos? |
Se trata de un sencillo ejercicio de movimientos constantes, y la principal enseñanza que va a dejarte es la siguiente: no es necesario realizar cambios de sistemas de referencia dentro de un ejercicio. Aunque pueda hacerse, y te resulte más fácil abordar cada uno de los movimientos que integran el ejercicio con un SR para cada uno, la dificultad que se suma por hacerlo íntegramente con un único SR no es dramática y te va a permitir familiarizarte con esa herramienta magnífica que es la ecuación horaria.
| |
|
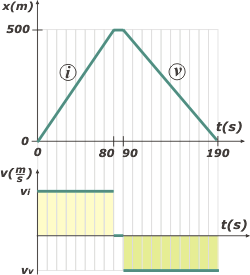 |
Voy a usar el subíndice i para ida y el subíndice v para vuelta.
Siempre que tengo que hacer un gráfico lo acompaño por otro (u otros) que complete la información. Pero siempre los ordeno encolumnados de la misma manera: posición arriba, le sigue velocidad y -cuando vale la pena- aceleración abajo de todo. Por supuesto, los tres con la misma escala de tiempo. A esta configuración la llamo tándem.
A falta de esquema, los gráficos me ayudan a comprender el problema, ponerle nombre (o números) a los datos o incógnitas del ejercicio... y armar las ecuaciones horarias. |
|
|
|
Ahora tengamos a mano el modelo de ecuación horaria que vamos a usar:
x = xo + v ( t – to )
Para armar las ecuaciones de los corredores necesito tres constantes de cada movimiento: la velocidad, una posición (voy a tomar el inicio) y el instante de tiempo que se corresponde. Quedan así: |
|
|
| ida |
x = vi . t
|
Abajo hay otro recuadrito amarillo en el que te hago un comentario sobre estas ecuaciones |
| vuelta |
x = 500 m + vv ( t – 90 s)
|
|
|
|
| A estas dos ecuaciones -cada una- que describen totalmente el movimiento de cada tramo, les vamos a pedir que hablen exclusivamente de la posición y el instante de las metas, que son las que indica el enunciado. Fijate: |
|
|
 |
500 m = vi . 80 s
|
[1] |
0 m = 500 m + vv ( 190 s – 90 s)
|
[2] |
|
|
|
Inevitablemente desembocás en un sistema de tantas ecuaciones como incógnitas (en este caso: 2 y 2). Acá terminó la física del problema. Lo que queda es álgebra. No llores, yo te lo hago. Con la ecuación [1] calculo vi... |
|
|
|
|
|
Con la ecuación [2] calculo vv... |
|
|
|
|
|
Las preguntas siguientes se las formulo a las ecuaciones que describen los movimientos. Lógicamente: si quiero preguntar por la posición en un instante en que el corredor todavía está yendo, se lo pregunto a la ecuación de ida; por un instante en que está volviendo, a la ecuación de la vuelta. Las ecuaciones son solícitas... pero ingenuas... ellas responden siempre, les corresponda o no. Tené cuidado con eso.
x40s = 6,25 m/s . 40 s
|
|
|
| |
|
|
x125s = 500 m – 5 m/s ( 125 s – 90 s)
|
|
|
|
|
|
| Para saber en qué posición estaba el corredor en el instante 85 s, no necesitás resolver ninguna ecuación. Si leíste el enunciado atentamente sabés que en ese instante el corredor está recuperando energía en los 500 m. Para ese intervalo no hay ecuación horaria porque la posición es constante durante esos 10 segundos de descanso, no depende del tiempo. |
|
|
| Comentario: esas dos ecuaciones (funciones) nadie las escribe. Ningún libro con ejercicios resueltos, ningún apunte de ejercicios resueltos, ningún profesor en su clase, ningún estudiante en su práctica ni en su examen... Todos las saltean y van directamente a las dos que siguen, que yo llamé [1] y [2]. ¡Y son la parte más substanciosa de la física! ¡Son las expresiones que describen todo el movimiento, todo el fenómeno natural! ¡Como profesional de la salud NUNCA vas a tener que calcular encuentros de automóviles! En cambio... vas a tener que enfrentar fenómenos naturales que se DESCRIBEN con funciones como las que tenés ahí. Llevate eso; la cinemática es sólo una excusa. |
|
|
|
| |
|
 |
| |
|
| DESAFIO: ¿Cómo son entre sí las áreas que te sombreé en el gráfico de velocidad-tiempo, y cuánto valen? ¿Te animás a escribir una ecuación horaria para el tramo entre el segundo80 y el 90? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco a Sol Albanese la detección de un error en este ejercicio. Última actualización jul-08. Buenos Aires, Argentina. |
|
|
| | |
|
|

