NO ME SALEN
PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC
(Movimiento uniforme)
|
|

|
| |

|
|
2- Un ciclista que viaja en una trayectoria
rectilínea recorre la primera mitad de su camino
a 40 km/h y la otra a 20 km/h. Despreciando el
tiempo empleado en variar la velocidad, |
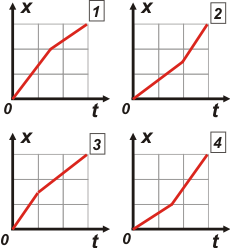
| a) ¿cuál de los siguientes gráficos de posición
en función del tiempo representa el movimiento? |
|
|
 |
|
|
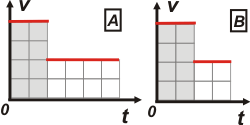
b) ¿cuál de los si guientes gráficos de velocidad
en función del tiempo representa el movimiento? |
|
|
 | |
|
c) El otro gráfico de v(t), ¿con cuál de los gráficos
x(t) se corresponde? Describa la situación
correspondiente a estos gráficos.
d) Observando las áreas bajo los respectivos
gráficos de v(t) analice la veracidad o falsedad de
la siguiente expresión de la velocidad media:
vm = (v1 + v2)/2 |
|
|
Bonito ejercicio... Y sencillo. Te ayuda a interpretar correctamente los gráficos y aprender un par de cosas importantes. Prestá atención.
El enunciado afirma que el ciclista va primero a 40 y después a 20 (las unidades no importan ahora). Pero no cabe duda que primero va más rápido y después más lento. En el ejercicio anterior habíamos visto que la inclinación de la gráfica posición-tiempo es indicativo de la rapidez. O sea: más inclinado más rápido, menos inclinado, más lento. Si entendiste esto tenés que elegir un gráfico cuyo primer tramo esté más inclinado y el segundo menos. Los posibles son los 1 y 3 y los que debés descartar de plano son el 2 y el 4. |
|
|
 |
|
|
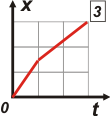
Entre el 1 y el 3 también es sencillo, aunque a alguna gente le pueda parecer sutil. El enunciado dice que recorre la primera mitad de su camino... bla, bla, bla. El camino es lo que se ve en el eje x, el vertical. Y la mitad del camino aparece en la mitad del cuadradito del medio. El gráfico 1 representa un móvil que recorre los primeros dos tercis del camino a una velocidad y el último tercio a otra... no es nuestro gráfico. El nuestro es el 3.
|
|
|
 |
|
|
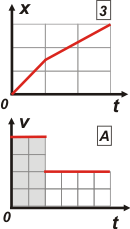
Para saber cuál de los dos graficos de velocidad tiempo se corresponde con el enunciado hay varias posibiidades. Una de ellas es analizar un poquito más el que acabamos de elegir posición-tiempo. Ahí podés ver que el primer tramo es más breve y el segundo, más largo. De ninguna manera ambos tiempos iguales (es obvio que si la segunda mitad se pedalea más lento se tardará más en cubrir la distancia). Luego, el correcto es el A y debemos descartar el B. Acá te los muestro en tandem:
|
|
|
 |
|
Para representar en tándem es importante que los gráficos encolumnados tengan la misma escala de tiempo, por eso tuve que toquetear un poquito uno de ellos (el de posición).
Otra caracterísitca importante de los gráficos velocidad-tiempo, que te va a ser muy útil en la vida, es la siguiente: el área encerrada bajo la curva representa el desplazamiento.
A ver. En el primer tramo (velocidad a 40 km/h) el área encerrada (que está grisada) son 8 cuadraditos. Y en el segundo tramo (velocidad a 20 km/h) el área encerrada también son 8 cuadraditos. ¡Eso coincide con nuestras expectativas! A saber, que las dos mitades del trayecto son iguales desplazamientos... si no, no serían mitades. |
|
|
|
c) El otro gráfico de v(t), ¿con cuál de los gráficos
x(t) se corresponde? Describa la situación
correspondiente a estos gráficos.
Bueno, se supone que con todo lo que aprendiste hasta acá podés responder esta pregunta sin mi ayuda.
d) Observando las áreas bajo los respectivos
gráficos de v(t) analice la veracidad o falsedad de
la siguiente expresión de la velocidad media:
vm = (v1 + v2)/2
¡Epa! Para responder esto tenés que saber qué es la velocidad media. Se trata del cociente entre el desplazamiento total (en nuestro caso las dos mitades) y el tiempo total insumido en ese desplazamiento. Si lo querés en otras palabras... es la velocidad constante e invariante a la que tendría que haber pedaleado un segundo ciclista que partiendo en el mismo instante que el nuestro habría llegado junto con él.
Es obvio que se tratará de una velocidad intermedia, comprendida entre la máxima y la mínima, o sea, entre 40 y 20... ¡Pero no el promedio! ¡No 30! O sea que la proposición del enunciado es FALSA.
El valor correcto lo hallás con esta fórmula: |
|
|
| vm= |
|
2 v1 v2 |
FÓRMULA COMPLEMENTARIA # 365 |
|
| ( v1 + v2 ) |
|
|
|
Que en nuestro caso arroja un valor de:
vm= 26,67 km/h
Si no lo creés, podés hacer unos cálculos mentales muy sencillos: ponele que nuestro ciclista tardó una hora exacta en hacer la primera mitad del recorrido que, obviamente, mide 40 kilómetros. Para hacer los 40 kilómetros restantes tardará dos horas, ya que lo hace a 20 kilómetros por hora. En total recorrió 80 kilómetros y tardó 3 horas. Hagamos la cuenta: |
|
|
| vm = |
|
80 km |
|
= 26,67 km/h |
|
| 3 h |
|
|
|
| Qué loco, ¿no? Ponele. |
|
|
|
|
|
PARA APRENDER MÁS:
- Si te picó el bichito de la curiosidad podés ver un ejercicio en el que está resuelto este mismo pero con otros valores. Acá está. Y ahí explico esa fórmula con la que calcular la velocidad media en circunstancias como ésta.
- En el gráfico de velocidad B, el que no representa a nuestro ciclista, ¿cuánto vale la velocidad media? ¿Podés resolverlo gráficamente?
|
|
 |
| |
| |
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-20. Buenos Aires, Argentina. |
|
|
| |
|
|
|

