CINEMATICA, apuntes teoricos, MRUV, practica online de fisica

home

más de cinemática

otros temas de Física

lecciones del maestro Ciruela

tonterías

NO ME SALEN
APUNTES TEORICOS DE FÍSICA Y BIOFÍSICA DEL CBC

manolito

Deducción de las ecuaciones horarias de posición y velocidad del MRUV

Como te mostré en el apunte anterior, las ecuaciones horarias del MRUV son:

x = x_o + v_o ( t – t_o ) + ½ a . ( t – t_o )²

v = v_o + a ( t – t_o )

(en rojo las variables en azul las constantes; que distingas eso es lo fundamental)

En este apunte te voy a mostrar por dos métodos diferentes de dónde surgen esas expresiones. En ambas tenemos que recordar que la velocidad es la derivada de la función posición y la aceleración es la derivada de la función velocidad.

Y como en ambos casos vamos a partir de la característica fundamental del MRUV, o sea, que la aceleración es constante,

a = cte

para llegar de ahí a la función velocidad y de la función velocidad a la de posición, tenemos que recorrer el camino inverso de la derivación, o sea, la integración.

Método gráfico

Este camino es muy sencillo. Fue justamente Newton quien se dio cuenta que integrar una función era lo mismo que calcular áreas encerradas bajo la curva de esa función.

De modo que para calcular un cambio de velocidad, ( v – v_o ) lo podemos hacer calculando el área encerrada bajo la curva de la aceleración entre los instantes t y t_o, donde t_o es un instante de referencia y t es un instante cualquiera (o sea, la variable).

Como se trata de un rectángulo hallar el área es una pavada: base por altura. La altura vale a y la base ( t – t_o). Entonces:

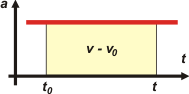
v – v_o = a ( t – t_o)

Que si lo mirás con cariño, no es otra cosa que la definición de aceleración media que te presenté en el apunte anterior.

De ahí despejamos la variable v y nos queda:

v = v_o + a ( t – t_o)

Que es lo que esperábamos. Como ves la función velocidad resulta lineal y su gráfica será una recta oblicua:

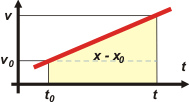
Y ahora, nuevamente, para conocer un incremento de posición (un desplazamiento), ( x – x_o), podremos calcular el área encerrada bajo la curva v, entre dos instantes -como antes- t y t_o.

Se trata de un área banstante simple, un trapecio, que se calcula como altura media por base. O si vos querés, para hacertela más sencilla, lo podemos dividir en dos áreas (mirá la línea punteada) un rectángulo abajo (base por altura) y un triángulo arriba (base por altura sobre 2).

x – x_o = (área del rectángulo) + (área del triángulo)

x – x_o = v_o ( t – t_o) + ½ ( v – v_o) ( t – t_o)

Como recordás del desarrollo anterior,

v – v_o = a ( t – t_o)

Entonces la ecuación la podemos escribir así:

x – x_o = v_o ( t – t_o) + ½ a ( t – t_o) ( t – t_o)

Con lo que arribamos a la ecuación que ya conocías:

x = x_o + v_o( t – t_o ) + ½ a ( t – t_o)²

Método analítico

Lo siguiente es lo mismo, pero en lugar de calcular áreas vamos a integrar analíticamente. Claro, tenés que tener ya un entrenamiento previo en análisis matemático (derivación e integración). Sólo lo básico (álgebra de integrales, reglas de integración de función potencial, integral definida y regla de Barrow).

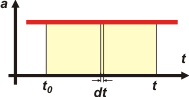
Consiste en realizar lo mismo que antes, pero en lugar de calcular las áreas de un plumazo, las vamos a dividir en infinitas columnas de base dt y después las sumamos todas sin perdernos ninguna (eso se llama suma integral o simplemente integral).

v – v_o=

∫

a dt = a t + C

= a t + C – a t_o– C

t_o

v – v_o= a ( t – t_o)

Ahora pasamos sumando v_o, y abracadabra...

v = v_o + a ( t – t_o)

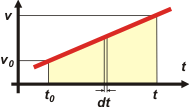
Para hallar la función posición vamos a hacer lo mismo, es decir integrar la función velocidad:

Cada columnita es apenas un rectángulo muy finito, pero un rectángulo al fin, ya que siendo la base tan estrecha (un infinitésimo, una nada) los lados verticales tienen la misma altura.

x – x_o=

∫

(v_o + a ( t – t_o )) dt = v_o t + ½ a t² – a t_o t + C

t_o

integro

x – x_o= v_o t + ½ a t² – a t_o t + C – v_o t_o – ½ a t_o² + a t_o² – C

x – x_o= v_o t + ½ a t² – a t_o t – v_o t_o – ½ a t_o² + a t_o²

x – x_o= v_o ( t – t_o) + a ( ½ t² –t_o t + ½ t_o² )

x – x_o= v_o ( t – t_o ) + ½ a ( t² – 2 t_o t + t_o² )

x – x_o= v_o( t – t_o ) + ½ a ( t – t_o)²

Despejamos x y ya:

Barrow

cancelo C

factor común por partes

aparece un trinomio cuadrado perfecto

x = x_o + v_o( t – t_o ) + ½ a ( t – t_o )²

¡Ya la ví tantas veces que me la acuerdo de memoria!

CHISMES IMPORTANTES:

Una de las cosas interesantes del método integral es que permite calcular áreas no geométricas, o sea, que no representen figuras conocidas.
dt, diferencial de tiempo, significa pequenísimo intervalo... cuánto de pequeño: tanto que es más chico que el menor intervalo que seas capaz de definir.

PREGUNTAS CAPCIOSAS:

¿Quiénes inventaron el análisis matemático?
¿De dónde viene el símbolo de la integral que parece una S estilizada?

Me embola escribir m/s (metro sobre segundo) de esa forma, con la raya oblicua. Lo correcto es escribir la m justo arriba de la s y con la raya horizontal. Lo mismo con ½. (Más información sobre esta cuestión aquí).