 |
NO ME SALEN
APUNTES TEORICOS DE FÍSICA Y BIOFÍSICA DEL CBC
|
|

|
Movimiento rectilíneo uniforme, MRU
Se trata del tipo de movimiento más sencillo que se pueda imaginar. Ideal para aprender a hacer cinemática. Su nombre lo caracteriza: la palabra rectilíneo indica que la trayectoria coincide con una recta; y la palabra uniforme que la velocidad, v, del móvil es constante.
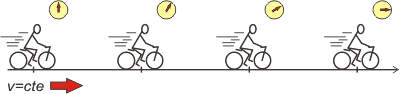
Por velocidad debés entender lo que siempre entendiste por velocidad (te lo pongo así porque -aunque no lo creas- el concepto de velocidad no es muy sencillo de definir matemáticamente... pero confío en que no hace falta: vos sabés a qué nos estamos refiriendo). Mirá el esquema: |
|
 |
|
Un móvil animado con un MRU se desplaza distancias iguales en tiempos iguales.
Un gráfico posición-tiempo típico de un MRU es el siguiente: |
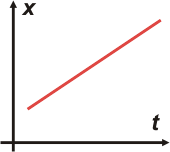 |
Cualquier recta oblicua bien puede representar un MRU. Si la inclinación es como ésta la llamamos ascendente o creciente y decimos que se trata de un movimiento de avance. Si la recta se inclina hacia abajo decimos que es descendente o decreciente y representa un movimiento de retroceso.
Si la recta fuese horizontal representaría un móvil que no cambia la posición, está detenido o en reposo. Aunque parezca ridículo también lo incluimos dentro de los MRU. La orientación prohibida es la vertical: indicaría que el móvil se encuentra en infinitas posiciones en un mismo instante... imposible. |
|
|
|
| Fijate que la recta no necesariamente debe pasar por la posición x = 0 en el instante t = 0. Inventemos un ejempo, cuyos datos voy a volcar es esta Tabla de Valores: |
|
|
| x (m) |
t (s) |
| 0 |
9 |
| -12 |
15 |
| 18 |
0 |
| 12 |
3 |
| 24 |
-3 |
|
Para inventar el ejemplo procedí de esta manera: hice un gráfico de un MRU sobre una cuadrícula procurando que coinciera con varios vértices. Después inventé una escala arbitraria y listo.
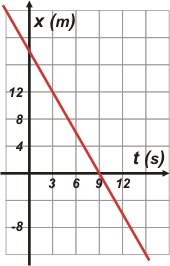
Si representamos los puntos en un gráfico aparece el que tenemos ahí abajo. Tratá de agregar vos tres o cuatro pares x-t simplemente con observar el gráfico. |
|
|
en matemática se le dice curva a cualquier gráfica... aún si se trata de una recta |
| Tal vez te diste cuenta que los pares que yo volqué en la tabla no tienen ningún orden preestablecido... La tabla de valores en una estantería para almacenar información relevante, pero en poca cantidad, para que sea fácil de buscar. |
|
|
 |
Ahora viene lo más saliente del MRU: si tomamos cualquier desplazamiento y lo dividimos por el intervalo de tiempo correspondiente a ese desplazamiento, siempre nos va a dar el mismo número; ese cociente es constante (independiente de los pares que elijas para considerar el desplazamiento y el intervalo)... ese cociente es la velocidad media, vm, (que en el MRU -y sólo en el MRU- concuerda con la velocidad propiamente dicha. |
| vm |
= |
Δx12 |
= |
x2 – x1 |
|
|
|
| Δt12 |
t2 – t1 |
|
Velocidad media igual desplazamiento sobre intervalo de tiempo correspondiente. Los subíndices sirven para remarcar esa correspondencia.
De la tabla de valores elijamos al azar dos pares cualesquiera y armemos el cociente. Por ejemplo el segundo y el tercer renglón de la tabla. |
|
|
Cuanto antes dejes de usar las palabras
final e inicial,
más rápido vas a aprender cinemática
|
| vm = |
|
– 12 m – 18 m |
|
= – 2 m/s |
|
| 15 s – 0 s |
|
|
|
Si lo hubiésemos armado al revés daba lo mismo: |
|
|
| vm = |
|
18 m – ( –12 m ) |
|
= – 2 m/s |
|
| 0 s – 15 s |
|
|
|
Lo importante es que respetes la correspondencia entre cada posición y su instante. Probá vos con cualquier otro par de pares sacados de la tabla y vas a ver que el cociente da siempre lo mismo. En el MRU -y sólo en él- no hace falta recordar que se trata de la velocidad media y lo vamos a llamar directamente velocidad, v.
La herramienta cinemática que describe con mayor precisión y generosidad los movimientos es la ecuación horaria. En los MRU tiene siempre esta pinta:
x = xo + v ( t – to )
x y t son las variables. Si no aparecen, fuiste; no hay ecuación horaria. El resto: xo , v y to , son constantes, o sea números. Con suerte te dan el valor de esas constantes. Si no te los dan, tal vez los puedas encontrar o quizás los puedas decidir vos. ¡Pero no son variables, son constantes! Es decir, una vez que te los dan, o que los encontrás, o que los decidís, ya está, son constantes, no cambian, valen siempre lo mismo... cómo querés que te lo diga...
En nuestro ejemplo de más arriba la velocidad era v = – 2 m/s, y podríamos tomar como xo y to los que figuran en el cuarto renglón de la tabla ya que el único requisito que deben tener xo y to es: corresponderse entre sí y pertenecer al movimiento. Nuestra ecuación quedaría así:
x = 12 m – 2 m/s ( t – 3 s )
eso es una ecuación horaria, no cabe duda, porque contiene x y contiene t. Además te puedo asegurar que xo = 12 m, v = – 2 m/s y to = 3 s.
También podríamos haberla armado eligiendo el quinto renglón de la tabla:
x = 24 m – 2 m/s ( t + 3 s )
|
|
|
| x (m) |
t (s) |
| 0 |
9 |
| -12 |
15 |
| 18 |
0 |
| 12 |
3 |
| 24 |
-3 |
| 8 |
5 |
|
Si a cualquiera de las dos ecuaciones (que en realidad son la misma) le hacemos la misma pregunta, nos darán la misma respuesta. Por ejemplo; dónde se hallaría el móvil en el instante t6 = 5 s... En cualquiera de las dos, donde dice t escribimos 5 s, luego hacemos la cuentita, y del otro lado del igual aparece x6 = 8 m.
Los agregué en el último renglón de la tabla. |
|
|
|
Fijate que siempre se puede distinguir qué es una constante y qué es una variable por la presencia de subíndice. t6 vale 5 s. Le puse 6 al subíndice porque había que ponerle un nombre, sólo por eso; se me ocurrió 6, pero se me podría haber ocurrido 10, A, Q... pero elegí 6. Luego x6 es la posición que se corresponde con ese instante. En cambio t es el símbolo de un conjunto infinito, representa a cualquier instante de tiempo, puede representar a to , t6 , tA , el minuto 34 o la hora 78.
Una ecuación horaria es una expresión capaz de decirte en qué posición se encuentra un móvil en cualquier instante de tiempo. Es un almacén de información cinemática, guarda infinitos pares de información posición-tiempo. Si de un movimiento cualquiera, vos conocés la ecuación horaria, ya está, ese movimiento no tiene más secretos para vos.
|
|
|
CHISMES IMPORTANTES: |
|
|
- La velocidad propiamente dicha, llamada velocidad real, (a veces también velocidad lineal o velocidad tangencial) no es un concepto sencillo de definir matemáticamente. Hay que hacer uso de herramientas matemáticas sofisticadas como el límite, o la derivada. Por suerte en el MRU no hace falta, porque coincide plenamente con el concepto de velocidad media, que matemáticamente es una pavada.
- ¿Por qué el modelo de ecuación horaria del MRU tiene la forma que tiene? Sencillamente, si la gráfica de un MRU es una recta oblicua, entonces la función matemática que describe ese movimiento no puede ser otra que la función de una recta... y eso es justamente lo que es.
- La inclinación de la recta (a los físicos les gusta llamarla pendiente) nos informa sobre la rapidez del movimiento: cuanto más inclinada más rápido es el movimiento; cuanto menos inclinada más lento es.
|
|
|
| PREGUNTAS CAPCIOSAS: |
|
|
- ¿Se podrá demostrar que las dos ecuaciones que escribí en este apunte son la misma? Entonces... será que cada movimiento tiene una y solo una ecuación horaria que lo describe... pero esa ecuación horaria se puede escribir de infinitas formas diferentes?
- ¿Qué movimientos de la naturaleza conocés, que sean MRU?
- La ecuación horaria del MRU es la ecuación de una recta. Y si hacés el gráfico posición-tiempo, lo que aparece es una recta. ¿Podría tratarse de una recta horizontal (paralela al eje de los tiempos)? ¿Podría tratarse de una recta vertical (paralela al eje de las posiciones)?
|
|
 |
| |
|
| Me embola escribir m/s (metro sobre segundo) de esa forma, con la raya oblicua. Lo correcto es escribir la m justo arriba de la s y con la raya horizontal. (Más información sobre esta cuestión aquí). |
|
| | |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización may-09. Buenos Aires, Argentina. |
|
|
 |
| | |
|
|
|

