NO ME SALEN
APUNTES TEORICOS DE FÍSICA Y BIOFÍSICA DEL CBC
Movimiento libres verticales
(caída libre, CL, y tiro vertical, TV)
Si se arroja un objeto (no importa si hacia arriba o hacia abajo) en forma vertical la trayectoria que describe será una recta vertical y recibe el nombre de tiro vertical. Lo mismo ocurre si, en cambio, simplemente se suelta un cuerpo, y en ese caso se llama caída libre. La única diferencia entre ambos es la velocidad inicial (nula en el segundo caso). Acá los llamaré movimientos libres verticales, MLV.
Se los llama libres porque durante el vuelo nada los empuja ni los retiene (al menos aparentemente). Y lo que ocurre es que estos movimientos de trayectoria vertical son de tipo acelerado, MRUV, con aceleración contante igual a g, de forma tal que si están subiendo lo hacen cada vez más lento y si están bajando lo hacen aumentando la rapidez.
La condición para que ocurra este movimiento particular que voy a describir aquí es que las dimensiones de la trayectoria no sean muy grandes y que la interacción con el aire (fundamentalmente el rozamiento) sea despreciable. Por ejemplo, si suelto un copo de algodón no va a tratarse de un MLV. Tampoco una tiza si sale disparada hacia arriba a 300 m/s.
Pero sí, por ejemplo, una piedra que asciende unos 20 metros. Por tradición a los sistemas de referencia verticales con los que estudiamos estos movimiento los llamamos y en lugar de x. |
|

|
| |
g = 9,8 m/s²
en No me salen usaremos el valor aproximado
g = 10 m/s²
(no nos gusta hacer muchas centas)
|
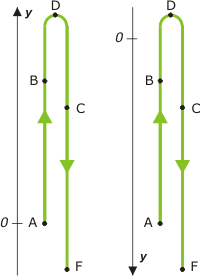 |
En los esquemas de No me salen, suelo representar los movimientos de subida y bajada de esta manera, valga la redundancia, esquemática, para que los eventos de la subida no se solapen con los de la bajada.
Elegís el sistema de referencia que más te guste, con el cero de las posiciones donde se te antoje, apuntando hacia arriba o hacia abajo, da lo mismo y le ponés un nombre arbitrario a todos los eventos que le ocurran al móvil y de los que vayan a hablar las ecuaciones.
Pero no te tenés que olvidar nunca de explicitar cuál es el sistema de referencia con el que estás describiendo el movimiento (ya sea con un esquema -como hace No me salen- o verbalmente). |
|
|
|
¿Por qué estos cuerpos se comportan de esta manera, por qué con aceleración constante y por qué con ese valor de aceleración? Ese es un asunto que podemos postergar porque ahora no viene al caso, pero que será dilucidado en los capítulos de dinámica.
En cinemática lo que nos interesa es describir el movimiento, es decir dar una expresión que nos cuente cuál es la posición de móvil en cualquier instante de tiempo. O sea una ecuación horaria.
En el caso de los MLV serán dos ecuaciones horarias que actuarán en forma conjunta:
y = yo + vo . ( t – to ) + ½ g . ( t – to )²
v = vo + g . ( t – to )
Ante cada MLV que enfrentes deberás ser capaz de armar dos ecuaciones como éstas. Para ello deberás encontrar (o decidir) cuatro constantes: to, yo, vo, g. Luego el movimiento no tendrá más secretos para vos. Todas las infinitas posiciones por las que pasa el móvil en cada instante de tiempo están ahí adentro, sólo hay que preguntar y aparecen.
Miremos este ejemplo. Supongamos que tenemos un tiro vertical que está descipto por estas ecuaciones (en las que to= 0 s, yo= 0 m, vo= 30 m/s, g = — 10 m/s²):
y = 30 m/s . t — 5 m/s² . t²
v = 30 m/s — 10 m/s² . t
Le voy a ir dando valores a t y obteniendo las posiciones y velocidades correspondientes a esos instantes. Y los voy volcando en la tabla. Por ejemplo donde dice t escribo –1 s, y hago las cuentitas. La de posición y(-1s) (tuve que escribir –1 s dos veces) da –35 m, y la de velocidad v(-1s) nos da 40 m/s. Y así. |
|
Las variables las representé en rojo y las constantes en azul.
|
| t (s) |
y (m) |
v (m/s) |
| -1 |
-35 |
40 |
| 0 |
0 |
30 |
| 1 |
25 |
20 |
| 2 |
40 |
10 |
| 3 |
45 |
0 |
| 4 |
40 |
-10 |
| 6 |
0 |
-30 |
| 5,5 |
13,75 |
-25 |
|
|
Vos podrías agregarles más preguntas a esas ecuaciones... por ejemplo en qué instante pasa por la posición metro 7, o dónde se halla en el instante 3,5 s, o en el segundo 168. Acordate que la ecuación no sabe cuándo empieza ni cuándo termina el movimiento. |
|
|
|
las tablas de valores no tiene por qué estar ordenadas (es preferible que no lo estén) |
También voy volcando los valores encontrados a los gráficos posición-tiempo, velocidad-tiempo y aceleración-tiempo (para cada eje). |
|
|
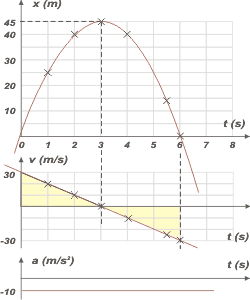 |
Las posiciones deberán ir alineándose en una parábola, lógicamente. Las velocidades en una recta oblicua y la aceleración en una recta horizontal.
El área encerrada bajo la curva en el gráfico velocidad tiempo representa al desplazamiento del móvil (esto vale para cualquier movimiento).
Este movimiento goza de varias simetrías respecto al instante en que el objeto alcanza (o alcanzaría) su altura máxima, que se corresponde con una velocidad igual a cero. Por ejemplo: lo que tarda en subir entre dos alturas cualesquiera es igaul a a lo que tarda en bajar entre esas dos mismas alturas. Otra: el módulo de la velocidad es el mismo a mismas alturas (de ida y de vuelta). |
|
|
las escalas de tiempo son iguales en cada columna de gráficos, eso recalca coincidencias importantes |
El signo de g. Hice un apartado especial para discutir el signo que lleva la aceleración, pero te adelanto que el signo de g solo depende del sistema de referencia que elijas, no depende de lo que haga el móvil, no importa si está subiendo o bajando o ambas cosas. ¡Ah! Y una cosa más: nunca cambies de sistema de referencia en medio de un ejercicio (está muy mal visto). |
|
|
|
|
|
CHISMES IMPORTANTES: |
|
|
- Cuando un cuerpo animado de un MLV llega a su punto más alto con velocidad igual a cero (podría no hacerlo si el movimiento se detiene antes) su aceleración sigue valiendo g.
- Cuando un cuerpo cae en el piso, la velocidad con la que toca el piso ¡no vale cero! De hecho, el la velocidad más alta de toda la bajada.
|
|
|
| PREGUNTAS CAPCIOSAS: |
|
 |
- ¿Todos los cuerpos caen con la misma aceleración?
|
|
| |
|
| Me embola escribir m/s (metro sobre segundo) de esa forma, con la raya oblicua. Lo correcto es escribir la m justo arriba de la s y con la raya horizontal. Lo mismo con ½. |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización jul-12. Buenos Aires, Argentina. |
|
|
 |
| |
|
|
|

