 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Funciones derivadas
|
|

|
| |
NMS a2.07 - Dada la
función
f(x) = x³ − 2x² − x + 2
a) encontrar las raíces
b) calcular la derivada primera de f(x) y evaluar para x = -1, x = 0, x = 1
c) calcular la derivada segunda de f(x) y evaluar para x = -1, x = 0, x = 1
d) observar los gráficos e interpretar las direivadas.
|
| |
Encontrar las raíces significa hallar los valores de x que hacen que la función valga 0. O lo que es lo mismo, hallar los puntos en los que la gráfica de la función corta al eje x. Como la función es cúbica podemos esperar hasta 3 raíces. Para hallarlas hay diferentes mecanismos, pero actualmente el más expeditivo es pedírselo a una calculadora cintífica (que tenga esa función) o a algún programa de computadora, o aplicación de teléfono. Las raíces son: |
|
|
| |
x1 = — 1 ; x2 = 1 ; x3 = 2 |
|
|
|
|
Derivemos sucesivamente para hallar la primera y segunda derivada, de un saque. La derivada de la función polinómica es lo más fácil que existe en el universo.
f(x) = x³ − 2x² − x + 2
f'(x) = 3x² — 4x — 1
f''(x) = 6x — 4
Hagamos los cálculos que nos piden. Primero la primera derivada: |
|
|
| |
f'(x) = 3x² — 4x — 1
f'(-1) = 6
f'(0) = — 1
f'(1) = — 2 |
|
|
|
|
| Segundo la segunda derivada: |
|
|
| |
f''(x) = 6x — 4
f''(-1) = — 10
f''(0) = — 4
f''(1) = 2 |
|
|
|
|
| Hagamos los gráficos, verifiquemos que los cálculos que hicimos son los correctos, y finalmente interpretemos lo que podamos. |
|
|
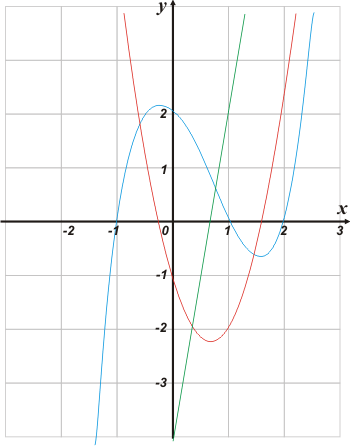 |
En azul la función original, en rojo su derivada primera (una parábola) y en verde la segunda (una recta).
Fijate primero los valores calculasdos, las raíces y las evaluaciones siguientes.
Qué cosas podemos interpretar... voy tirndo cosas que se me ocurren a mí y que me parecen dignas de mencionar. En las raíces de la parábola (f'(0)) la función tiene pendiente igual a cero lo que se corresponde con un máximo y un mínimo local.
A su vez, cuando la recta corta el eje x, la parábola tiene su mínimo, y obviamente pendiente nula. |
|
|
|
Podés revisar esto otro: la derivada de una función te va contando cómo varía la pendiente de su función primitiva. Hacé el esfuerzo de mirarlo, dale. |
|
|
| |
|
|
| DESAFIO: Hallar las raíces de la parábola. |
|
 |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| | |
|
|

