 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Funciones derivadas
|
|

|
| |
NMS a2.04 - Dada la
curva
f(x) = x³ − 3x² − 9x + 5
hallar el máximo ángulo de inclinación entre los dos vértices.
|
| |
Este es una vuelta más de tuerca del ejercicio 2.12, te conviene hacerlo antes que éste. Ya recontra sabés que la derivada de una función representa la pendiente de la recta tangente en todo punto, o sea las pendientes de la función primitiva en todo su ancho. Derivemos, pues:
f(x) = x³ — 3x² — 9x + 5
f'(x) = 3x² — 6x — 9
|
|
|
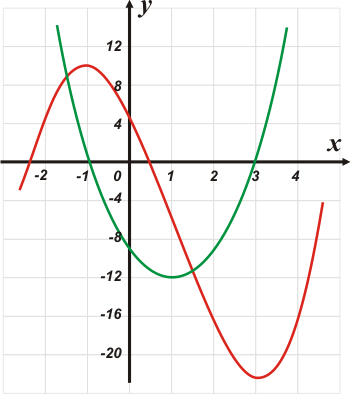 |
Este es el mismo gráfico que el del ejercicio 2.12, pero le cambié la escala para poder apreciar mejor algunos detalles.
La curva roja es la función primitiva, una típica cúbica. Y la curva verde su derivada, una cuadrática.
En el anterior habíamos visto que la derivada se hacía cero cuando la inclinación de la primitiva era nula: la derivada describe las pendientes. Y ahora buscamos en qué punto está más inclinada y cuánto vale esa inclinación. |
|
|
|
La gráfica de la derivada es una parábola y su valor mínimo (módulo máximo) es —12. Ese valor representa una pendiente máxima, αi, de:
αi = arc tg (—12)
|
|
|
|
|
|
Y eso ocurre en el punto que llamé Pi, cuyas coordenadas son:
xi = 1 y yi = —6
|
|
|
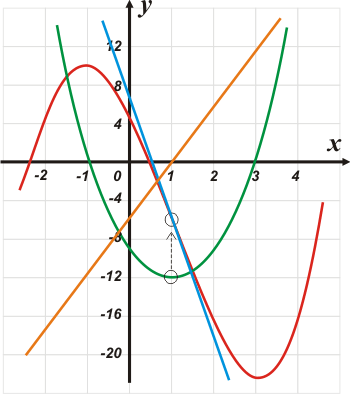 |
Ahí tenés la tangente (en azul) a la función en el punto en que su pendiente es máxima.
Fijate que pese a ser tangente también es secante... y eso tiene que ver con el siguiente comentario.
El hecho de que además de valer -12, se trate del vértice de la parábola (de la función derivada) nos indica que en ese punto la función cambia su concavidad. A izquierda concavidad negativa, a derecha concavidad positiva.
A eso se llema punto de inflexión (por eso elegí i)
Se trata de algo que describe correctamente la derivada de la derivada. |
|
|
|
En naranja te representé la derivada segunda de la función:
f"(x) = 6x² — 6
Que, como intuís, también describe cuestiones muy interesantes de la función primitiva. |
|
|
| DESAFIO: La recta celeste no parece estar inclinada 85,2 grados... casi 90... debería estar mucho más vertical que lo que muestra el gráfico ¿Nos está engañando Ricuti? |
|
 |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| | |
|
|

