 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Funciones derivadas
|
|

|
| |
FIS a2.05 - Calcular los puntos en que la tangente a la
curva
f(x) = x³ − 3x² − 9x + 5
es paralela al eje x.
|
| |
Este es un ejercicio súper clásico, si dobleces ni vericuetos. Ya recontra sabés que la derivada de una función representa la pendiente de la recta tangente en todo punto. Derivemos, pues:
f(x) = x³ — 3x² — 9x + 5
f'(x) = 3x² — 6x — 9
Y paralela al eje x significa sin inclinación, o sea, pendiente nula. Para hallar esas abcisas alcanza con pedirle a la función derivada que se anule:
0 = 3x² — 6x — 9
Esa ecuación se satisface para dos valores. Calculalos como quieras, ya sea con la formulita de los griegos: |
|
|
| |
xA , xB = |
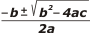 |
|
|
|
Donde a = 3, b = —6 y c = —9. O con una calculadora científica que tenga automatizada la búsqueda de raíces, o con una aplicación de computadora o de teléfono celular.
La solución es xA = —1 y xB = 3
Para conocer los puntos de tangencia nos faltan las ordenadas, ¡que hay que buscarlas en la función original, no es su derivada!
yA = xA³ — 3xA² — 9xA+ 5
yB = xB³ — 3xB² — 9xB+ 5
Vos hacé las cuentas |
|
|
|
|
|
| Mirá, te muestro el gráfico superpuesto de la función y su derivada. |
|
|
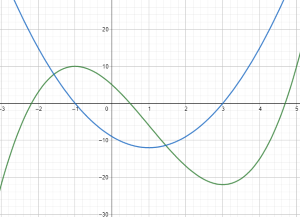 |
En verde la función original y en celeste su derivada.
Mirá la ubicación de los puntos A y B. Fijate que la curva celerste corta el eje de las x, justo en la abcisa en que la verde se pone horizonta. |
|
|
|
| |
|
|
| DESAFIO: ¿Cuáles son las raíces de la función original? |
|
 |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| | |
|
|

