 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Análisis matemático
|
|

|
| Funciones integrales |
| |
Dada una función cualquiera, su función primitiva (o integral o antiderivada) es aquella de la cual deriva. Por ello integrar es la operación inversa de derivar. Pero esto tiene un inconveniente: si bien la derivación es un camino directo a un destino único, la integración no lo es. Ya que infinitas funciones primitivas tienen la misma derivada. Por suerte todas ellas difieren entre sí en -solamente- una constante.
Simbólicamente: la derivada de P1 es D, la derivada de P2 es D, la derivada de P3 es D. ¿Cuál es la primitiva de D? Puede ser P1, o P2, o P3 o infinitas otras. Lo bueno es que P1, P2, y todas ellas difieren entre sí sólo en una constante, C.
Cálculo de áreas. Siendo la integración (dada una función cualquiera hallar la función de la cual deriva, de ahí viene su nombre primitiva) una operación que vincula funciones derivadas entre sí basta y sobra para encumbrar a la integración como una de las operaciones predilectas de la física. Sin embargo la integración le deparó a la humanidad una sorpresa adicional: el cálculo de áreas.
Resulta que la operación que realizamos al integrar es exactamente la misma que la que usaríamos para hallar un área de esta forma tan particular:
Sea una función cualquiera f(x)cuya representación es ésta: |
| |
|
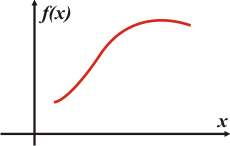 |
Y quisiésemos hallar el área encerrada bajo la curva entre dos x cuales quiera, xA y xB.
No es una operación sencilla, porque no se trata de un área geométrica típica del estilo de un rectángulo, un trapecio, un triángulo ni nada que se le parezca y cuyos cálculos de área ya resolvieron los griegos hace 2500 años. |
|
|
|
No, es una forma medio loca como un rectángulo uno de cuyos lados es curvilíneo y representa una función -al menos- conocida, f(x). |
|
|
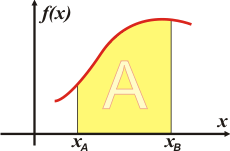 |
Acá te represento el área, A, que queremos conocer.
Un método no exacto pero muy práctico de encontrar un valor aprovimado del área consiste en dividir el intervalo entre xA y xB en intervalos menores todos iguales y construir con ellos rectángulos que tengan como base el intervalito que surge de la división y por altura el valor medio que adquiere la función dentro del intervalito. |
|
|
|
Mirá el siguiente gráfico: |
|
|
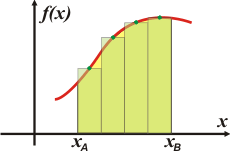 |
Las áreas de esos cuatro rectángulos es fácil de conocer (conociendo f(x) para cualquier x (los puntos verdes), y conociendo el intervalo etre xA y xB... es una operación de niños): base por altura. Luego si sumamos esas cuatro áreas, obtenemos una aproximación bastante decente del área original que queríamos encontrar.
Pero claro, es una aproximación, tan sólo eso. |
|
|
|
Pero podemos afinar la puntería si hacemos que los intervalitos en los dividimos el intervalo entre xA y xB sean muchos más y más pequeños. Claro, en ese caso la cantidad de rectangulitos (ahora mucho más flaquitos) que hay que sumar va a ser mucho mayor. Y aún así no dejaría de ser un cálculo aproximado, más aproximado que antes, pero aproximado al fin.
Y acá viene el salto al infinito que propone el cálculo: si el intervalito tendiese a cero (la base de cada rectangulito tendiese a cero) entonces la suma que tengo que realizar tendería a infinito... infinitos rectangulitos. Eso es mucho trabajo... pero el error que cometo en esa aproximación al área que estamos buscando se hace cero.
Además Newton y Leibniz desarrollaron un método muy económico para realizar esas sumas con infinitos términos (en nuestro caso, infinitos rectangulitos). Y lo llamaron suma integral. Y lo simbolizaron con una S alargada, justamente por suma. El área exacta es entonces: |
|
|
|
|
|
| Donde ∫ significa "la suma infinita", f(x) es la función "que estamos integrando" y dx (diferencial de x) es la base de nuestros rectangulitos, Δx, o sea variaciones de x tan pero tan minúsculas que tienden a confundirse con un cero. |
|
|
|
|
|
Cuando Newton descubrió que al llevar a cabo esta estrategia para el cálculo de áreas, realizaba la misma operación que para obtener la primitiva saió corriendo de su casa desnudo y gritando eureka, eureka... (o ese era otro y me estoy confundiendo). La cosa es que dada una función g(x) y su derivada, g'(x), se cumple que: |
|
|
|
|
|
A la expresión anterior se la conoce como integral definida, debido a que se hallan explícitos los límites de la suma integral: xA y xB. Pero los límites no son necesarios para hallar relaciones (de derivación) entre funciones. Entonces tenemos la integral indefinida:
g(x) = ∫ g'(x) dx
Pero alertados de problema de la no reversibilidad de la relación derivación-integración de la que te advertí en el principio de esta lección vamos a tener el cuidado de aclarar la diferencia de las constantes entre las funciones posibles g(x) de las cuales derivar g'(x).
∫ g'(x) dx = g(x) + C
Regla de Barrow
Volvamos a la integral definida. Se llama integral definida a aquella que tiene los extremos de la variable definidos (o sea: dos valores) en nuestro ejemplo xA y xB. Para hallar el área entre esos dos valores extremos se aplica la regla de Barrow: restar la integral en el valor superior menos la integral en el inferior. Eso se simboliza con una recta vertical y la indicación de los valores extremos: |
|
|
| |
|
∫ |
xB |
g'(x) dx = g(x) + C |
|
xB |
= g(xB) + C – g(xA) – C |
| |
|
| xA |
xA |
|
|
|
| Como ves, en la operación que propone Barrow la constante de integración (valga lo que valga) se cancela ya que es la misma y nos queda: |
|
|
| |
|
∫ |
xB |
g'(x) dx = g(xB) – g(xA) |
|
|
| |
| xA |
|
|
|
Bueno, en la ejercitación adjunta tenés suficiente material como para dotar de sentido este jeroglífico inmundo que te acabás de morfar. Que te aproveche. |
|
|
| Nota: si te apetece un poquito más de jerga-físico matemática te recomiendo esta nota que escribió mi buen amigo el Maestro Ciruela. |
|
 |
Chismes importantes
|
|
- El método de hallar áreas complicadas dividiéndolas en áreas pequeñitas fáciles de calcular y luego sumándolas todas, ya había sido puesta en práctica -y con mucho éxito- por Arquímedes y otros griegos brillantes. Lamentablemente fueron eclipsados por Aristóteles que podría ser un filósofo convincente, pero en cuestiones de ciencias era un papanata.
- Newton fue el descubridor del cálculo de áreas por el método de la integral. Pero parece ser que el que le advirtió que la integración era la operación inversa de la derivación fue su tocayo Isaac Barrow. ¿Lo ubicás?
- El teorema que demuestra que el cálculo de áreas por el método de las sumas infinitas es lo mismo que la operación inversa de la derivación se denomina: teorema fundamental del cálculo.
|
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| | |
|
|

