NO ME SALEN
(APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
CALOR Y TERMODINÁMICA
|
|

|
 |
Adicional NMS 27 - En base al ejercicio 37 (del experimento de Joule) hallar la variación de entropía entre el estado inicial y final por dos caminos reversibles diferentes. |
|
| |
¿Pero... si es reversible, la variación de entropía no tiene que ser nula? Pregunta muy interesante. Por ahora te la respondo así: NO. Y al final trataré de aclararlo como corresponde. Primero resolvamos el ejercicio. |
|
|
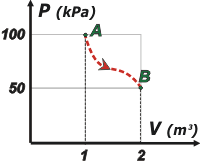 |
Como recordarás, el experimento de Joule consistía en descomprimir un gas ideal que pasa a ocupar un compartimiento anexo en el que previamente se había hecho vacío.
La clave del asunto (un poco tramposo para el iniciado) es que no hay trabajo alguno en expandirse en el vacío... el gas no debe empujar nada, no presiona un émbolo ni otro gas ni nada. No hay trabajo. |
|
|
Pot = ΔE/Δt |
Los textos suelen representar una evolución de ese tipo de esta manera, con una línea punteada. Pero esa línea punteada tiene un significado más profundo y es el siguiente: durante la evolución los estados intermedios están indefinidos. En una expansión abrupta como la del experimento de Joule, las presiones, los volúmenes y las temperaturas intermedias son imposibles de calcular. Incluso es muy probable que no sean uniformes en toda la masa del gas.
La entropía es una función de estado, de modo que la variación de entropía (que es lo que nos interesa) es independiente del "camino" por el que pasó el gas entre esos dos estados. Eso nos permite hacer el cálculo de la variación de entropía asumiendo un camino reversible cualquiera (con estados intermedios definidos).
La elección del camino es arbitraria pero, por supuesto, elegiremos una camino sencillo para facilitar el cálculo. Probemos primero con una evolución isotérmica.
|
|
|
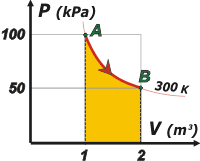 |
Acá tenés el gráfico de esa evolución en la que, como era de esperarse, queda un trabajo definido bajo la curva. representé -ya que estaba- la isoterma de 300 K.
En número de moles del gas lo podemos calcular con la ecuación de estado:
n = PA VA /R T
n = 100 kPa 1 m³ /8,314 J/K mol . 300 K
n = 40 moles |
|
|
|
El cálculo de la variación de entropía de las evoluciones estándar conocidas lo tenés acá. Y resulta:
ΔSAB = n R ln (PA /PB)
O lo que es lo mismo:
ΔSAB = n R ln (VB /VA)
Usemos la última:
ΔSAB = 40 mol . 8,314 J/K mol . ln (2 m³/1 m³)
ΔSAB = 40 . 8,314 J/K. ln 2
|
|
como
TA = TB
entonces
PAVA = PBVB |
|
|
|
|
Para que te convenzas de que la elección del camino reversible es arbitraria, hagamos un nuevo cálculo.
Ahora probemos por otro camino, también definido. Consiste en una evolución isocórica disminuyendo la temperatura hasta 150 K y la presión hasta 50 kPa. A ese estado intermedio lo denominé M. Luego una expansión isobárica hasta el estado B. |
|
|
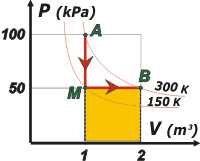 |
Acá tenés el gráfico. También te representé la isoterma de 150 K, pero -como antes- sólo a los efectos ilustrativos.
La variación de entropía desde el estado A hasta el B, tendremos que calcularla como suma de las variaciones de entropía de las evoluciones intermedias:
ΔSAB = ΔSAM + ΔSMB
|
|
|
|
ΔSAB = cV n ln (PM /PA) + cP n ln (VB /VM)
Recordando que se trataba de un gas ideal monoatómico, cV = 1,5 R y cP = 2,5 R.
ΔSAB = 1,5 R n ln (50 kPa/100 kPa) + 2,5 R n ln (2 m³/1 m³)
ΔSAB = 1,5 R n ln (0,5) + 2,5 R n ln (2)
ΔSAB = – 345,8 J/K + 576,3 J/K
|
|
|
|
|
|
Como ves, llegamos al mismo resultado que antes. Y no debe sorprenderte ya que la entropía es una función de estado, de modo que la diferencia de entropía entre dos estados cualesquiera no depende de cómo ocurrió la transformación para llegar de un estado a otro (aunque para calcularlo debas recurrir a una evolución definida, reversible) que no es la que realmente sufrió el gas.
Cuando llamamos reversible a una evolución de un sistema queremos indicar que el medio podría -en una situación ideal- variar su entropía en la misma cantidad y con signo contrario de forma tal que la entropía del universo no varíe. Pero sería más propio llamarlo definido o mejor aún cuasiestable, para evitar la confusión de que por sí solo, el sistema, sea reversible. |
|
 |
| |
|
| |
|
Desafío:
¿Podrías buscar un camino definido alternativo más? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Cuenta la historia que gran parte de lo que sabemos hoy sobre la termodinámica es gracias a que William Thomson pasaba mucho tiempo discutiendo con Lord Kelvin. Última actualización oct-12. Buenos Aires, Argentina. |
|
|
| |
|
|
|

