 |
NO ME SALEN
(APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
CALOR Y TERMODINÁMICA
|
|

|
| |
Adicional NMS 3 - Calcular la constante solar (CS, la cantidad de energía solar que llega a la Tierra por unidad de tiempo y de área), y la irradiación promedio (Ip, la recepción promedio en la superficie terrestre) conociendo el radio solar, la distancia entre el Sol y la Tierra y la temperatura de la superficie del Sol. |
|
| |
Acá tenemos otro ejercicio interesantísimo en el que con unos pocos datos, y aplicando la Ley de Stefan-Boltzmann te podés enterar del valor del subsidio solar (así lo llama el físico argentino Salvador Gil por tratarse de un flujo de energía absolutamente gratuito).
Primero voy a presentar los datos y algunas definiciones importantes que usaré luego, así no interrumpo el desarrollo del problema. Acá van:
Sol: el radio del Sol, RS, vale 700 mil kilómetros; con ese dato podemos calcular el área de su superficie, SS. (Acordate que el área de una superficie esférica, S, es igual a: S = 4π . R²).
RS = 6.7 x 108 m
SS = 5,64 x 1018 m²
Tierra: el radio de la Tierra, RT, vale 6.400 kilómetros; con ese dato podemos calcular el área de superficie terrestre, ST; y el área de el disco de sombra, DT, que después te explico para qué sirve... pero que se trata de un disco circular que tiene el mismo radio que la Tierra. (Acordate que el área de un círculo es igual a: A = π R²).
RT = 6,4 x 106 m
ST = 5,15 x 1014 m²
DT = 1,29 x 1014 m²
Esfera de órbita: Supongamos la existencia de una esfera hueca que tuviera su centro en el Sol y un radio igual a la distancia entre el Sol y la Tierra, o sea, igual al radio de órbita de la Tierra, RO. Ese radio vale 150 millones de kilómetros; y el área de esa esfera, EO, se calcula como el de cualquier otra esfera.
RO = 1,5 x 1011 m
EO = 2,83 x 1023 m²
|
|
|
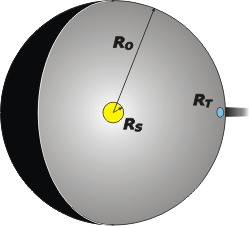 |
El esquemita, tal vez, te ayude a entender los conceptos que presenté y para qué voy a usarlos. La esfera grande gris, EO, es esa en la que el Sol reparte generosamente su energía radiante. (Ya sabemos que no hay tal esfera ni menos aún una superficie reflectante... pero la ponemos ahí sólo para hacer una medición).
El disquito azul es una Tierra chata, y sirve para cuantificar la cantidad de luz que la Tierra ataja. No importa qué relieve tenga la Tierra (ya sabemos que es esférica) lo que importa es cuánto captura... o, si querés, qué sombra proyecta. |
|
|
|
Ahí te dibujé un cachito de la sombra terrestre: es la sombra de un disco que tiene el mismo diámetro que la Tierra.
La potencia con que el Sol irradia hacia todos lados... eso se lo podemos preguntar a Stefan y a Boltzmann, que dirán:
PotS = σ . ε . SS . TS4
donde σ es la constante de Boltzmann, ε es el coeficiente de emisión que podemos aproximar a 1; SS es la superficie del Sol (desde donde irradia) y que ya sabemos cuánto vale. Y TS es la temperatura de esa superficie que como cualquiera sabe vale 5.900 kelvin.
PotS = 5,67 x 10-8 W/m² K4 . 1 . 5,64 x 1018 m² (5.900 K)4
PotS = 3,87 x 1026 W
Ahora bien, toda esa energía que sale del Sol se reparte para todos lados... la mayor parte se extravía en el espacio y una ínfima parte capturamos cuando nos ilumina. Nosotros -la Tierra- funcionamos como una pantalla para capturar la luz solar. Si estuviésemos más cerca atajaríamos más luz... y si estuviésemos más lejos menos. A la distancia que nos encontramos -un radio de órbita- para conocer la cantidad de radiación por unidad de área que capturamos debemos dividir la energía solar por el área de la esfera de órbita. Eso no es otra cosa que la constante solar, CS.
CS = PotS / EO
CS = 3,87 x 1026 W / 2,83 x 1023 m²
|
|
|
|
|
|
Pero momento a momento sólo hay un metro cuadrado en la Tierra que recibe justo esa cantidad de energía: es el metro cuadrado que está directamente apuntando al Sol... aquel que tiene el Sól en su cenit. Todos los demás cachos de Tierra están más inclinados y por lo tanto reciben menos luz (o incluso están del lado nocturno y no reciben nada.
La magnitud que describe el reparto equitativo de la radiación solar podemos llamarlo irradiación promedio, Ip, y la podemos calcular de varias maneras. Una de ellas es multiplicar la contante solar por el área de la "pantalla Tierra", DT, y dividirlo por el área total de la Tierra, ST. (Es lo mismo que dividir por 4).
Ip = CS . DT / ST
Ip = CS / 4
|
|
|
|
|
|
Que resulta ser un valor muy cercano al que te aparece en el ejercicio 19 de termodinámica y por ahí no entendiste de qué se trataba.
Comentario: 342 W/m² es un valor promedio... es obvio que no todas las áreas terrestres reciben la misma cantidad de Sol. En los polos se recibe muy poco entre los trópicos mucho más. También hay variaciones diarias (de noche no recibimos nada y durante el día va cambiando. También hay variaciones con las estaciones del año. Pero el factor más importante de corrección de ese valor es la reflexión de la Tierra. La atmósfera y la superficie del agua son muy reflectantes, de modo que sólo el 70% ingresa efectivamente a la tierra. El equilibrio radiante terrestre se llama albedo. |
|
|
| |
|
|
Chisme: los equilibrios energéticos de la Tierra son tan delicados que una pequeña diferencia en la reflectancia puede causar una catástrofe térmica como por ejemplo producir una era glacial. En la actualidad estamos más cerca de una catástrofe de signo contrario: un calentamiento global por efecto invernadero. |
|
|
| |
|
 |
|
|
| |
|
Desafío: ¿Cuánto vale la potencia radiante solar que la Argentina recibe en forma gratuita? |
|
| |
|
| Algunos derechos reservados (en criollo: no podés publicarlo a tu nombre, ¿entendiste? Mirá que tengo un boga repesado, ¿eh?).
Eso sí, se permite copiar, prestar, compartir y/o regalar este material... quedás como un duque. Última actualización ago-08. Buenos Aires, Argentina. |
|
|
| | |
|
|

