NO ME SALEN
(APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
CALOR Y TERMODINÁMICA
|
|

|
| |
|
 |
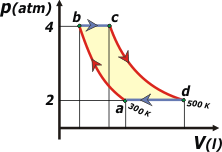
46) Para el ciclo descrito en el ejercicio 38 indique,
en el cuadro adjunto, sin efectuar cálculos, el
signo de la variación de entropía del gas, del
medio exterior y del universo para cada
evolución y para el ciclo completo. |
|
|
¿Hiciste el problema 38? ¿Te acordás del problema 38? En cualquier caso, andá y volvé. Te recuerdo que toda esa última parte en que hicimos los cálculos energéticos, no estaban previstos en el ejercicio y dependen de un dato que no figuraba en el enunciado, a saber: que el gas en cuestión era diatómico.
El asunto es que tenemos que estimar el signo de la variación de entropía; o sea, decir simplemente si ésta aumenta, disminuye o se mantiene constante. Es demasiado fácil, veamos: |
|
|
 |
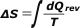
como el denominador es la temperatura absoluta, que siempre es positiva, el signo de la variación siempre depende del signo del calor: en definitiva, de si hubo calentamiento (ingreso de calor al sistema) o enfriamiento (salida de calor del sistema); en el primer caso será positivo, en el segundo negativo. |
|
|
|
Las evoluciones del ejercicio 38 son todas reversibles, definidas, de modo que el calor intercambiado es, justamente, lo que llamamos un calor reversible (podemos quedarnos tranquilos).
En la tabla siguiente te copié en el primer renglón el signo del calor en cada etapa del ciclo, tal como lo resolvimos en el problema 38. El segundo renglón es el signo de la variación de entropía del gas, ΔSG. |
|
|
| |
ab |
bc |
cd |
da |
ciclo |
| QG |
– |
+ |
+ |
– |
11,37 latm |
| ΔSG |
– |
+ |
+ |
– |
0 |
| ΔSM |
+ |
– |
– |
+ |
0 |
| ΔSU |
0 |
0 |
0 |
0 |
0 |
|
|
|
La variación de entropía del universo, ΔSU, (para la evolución de este gas) será nula en todo momento, ya que -es dato del ejercicio- se trata de una evolución reversible (acordate que una de las definiciones más trascendentes de la reversibilidad de un proceso cualquiera es que la variación de entropía del universo sea cero).
Luego el signo de la variación de entropía del medio, ΔSM, surge por inferencia de la relación:
ΔSG + ΔSM = ΔSU
Por otro lado: si el intercambio de calor se realiza entre el medio y el gas, la variación de entropía de ambos debe tener signo opuesto necesariamente.
Y ya que nos habíamos tomado el trabajo de inventar un dato para poder realizar cálculos numéricos, repitamos la hazaña y calculemos -numéricamente- las variaciones de entropía. En los tramos isotérmicos es sencillo: basta con dividir el calor intercambiado por la temperatura de la evolución. Y en los tramos isobáricos (no te asustes: tampoco aquí necesitás integrar, ya lo hice yo) usaremos:
ΔSG = cp n ln (TF /T0 )
|
|
|
| |
ab |
bc |
cd |
da |
ciclo |
| QG (l.atm) |
–17,05 |
57,40 |
28,42 |
–57,40 |
11,37 |
| TG (K) |
300 |
300 → 500 |
500 |
500 → 300 |
ΔT = 0 |
| ΔSG (l.atm/K) |
–0,05684 |
0,1467 |
0,05684 |
–0,1467 |
0 |
|
|
|
Y cartón lleno.
Advertencia: cualquier uso que se dé a este información producirá un aumento de la entropía del universo, con el consiguiente aumento del desorden. Si bien el estudiante no tiene la culpa de ello, le advertimos que este proceso conducirá a la muerte térmica del universo. |
|
|
| |
|
 |
| Desafío: Por favor, recalculame calores en joules, y entropías en joules por grado kelvin. Gracias. |
|
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. El juego de la entropía: no puedes ganar, no puedes empatar, no puedes abandonar. Última actualización nov-07. Buenos Aires, Argentina. |
|
|
 | |
|
|

