 |
NO ME SALEN
(APUNTES TEÓRICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
CALOR Y TERMODINÁMICA
|
|

|
| |
 |
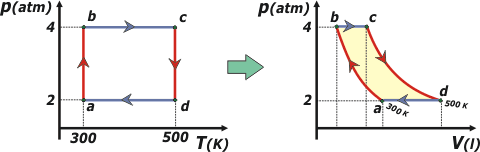
38) Un mol de gas ideal evoluciona cumpliendo el ciclo de la figura, en sentido abcda.
a) Efectúe el gráfico de presión en función de volumen.
b) En el cuadro adjunto indique, sin efectuar cálculos, los signos del trabajo y del calor
intercambiados y de la variación de energía interna del gas, en cada evolución y en el
ciclo. |
|
| |
Laborioso... pero hay que hacerlo. Para confeccionar el gráfico correctamente tenemos que conocer los volúmenes correspondientes a los cuatro estados a, b, c y d. Vamos entonces a recurrir a la ecuación de estado de los gases ideales (P V = n R T)... que para eso nos indican que se trata de un gas ideal.
Va = n R Ta / Pa =
Va = 1 mol . 0,08207 (lt atm/mol K) . 300 K / 2 atm = 12,3 lt
Vb = n R Tb / Pb = 6,15 lt
Vc = n R Tc / Pc = 10,25 lt
Vd = n R Td / Pd = 20,5 lt
|
|
|
 |
|
|
| Te dibujé las evoluciones correspondientes de ambos gráficos en distintos colores: rojo las isotérmicas, y morado las isobáricas. Ahora vamos a ir llenando el cuadro de a poco. Te voy a ir contando cómo deducimos cada signo. El orden en que yo lo hago no necesariamente sigue alguna lógica. |
|
|
| La variación de energía interna en evoluciones isotérmicas es nula. Lo mismo ocurre para los ciclos cerrados ya que el gas parte y regresa al mismo estado. |
| |
ab |
bc |
cd |
da |
ciclo |
| Q |
|
|
|
|
|
| L |
|
|
|
|
|
| ΔU |
0 |
|
0 |
|
0 |
|
|
|
|
| Los trabajos son positivos si aumenta el volumen del gas, y negativos si disminuye. Para el ciclo cuenta si se recorre en sentido horario o antihorario. En este caso es horario y, por lo tanto, positivo. |
| |
ab |
bc |
cd |
da |
ciclo |
| Q |
|
|
|
|
|
| L |
– |
+ |
+ |
– |
+ |
| ΔU |
0 |
|
0 |
|
0 |
|
|
|
|
El signo de las variaciones de energía interna que no son nulas, depende del signo de ΔT. Entonces: ΔUbc > 0 y ΔUda < 0.
El resto ya lo podríamos deducir aplicando ΔU = Q – L. |
| |
ab |
bc |
cd |
da |
ciclo |
| Q |
|
|
|
|
|
| L |
– |
+ |
+ |
– |
+ |
| ΔU |
0 |
+ |
0 |
– |
0 |
|
|
|
|
De todos modos podemos verificar sabiendo que el signo del calor depende siempre del aumento o disminución de la temperatura... algo que sabés desde que aprendiste calorimetría. |
| |
ab |
bc |
cd |
da |
ciclo |
| Q |
– |
+ |
+ |
– |
+ |
| L |
– |
+ |
+ |
– |
+ |
| ΔU |
0 |
+ |
0 |
– |
0 |
|
|
|
|
| Vamos a hacer una cosa que no estaba en los planes de la guía. Calculemos las cantidades del cuadro, no solo su signo. Ojo, para ello vamos a tener que inventar un dato que el enunciado no proporciona: supongamos que se trata de un gas diatómico, de modo que su calores específicos molares valen: cV = 2,5 R y cP = 3,5 R. Hacelo solo. Abajo completé el cuadro con mis resultados (que además nos van a servir para el ejercicio 46) expresados en lt.atm. En la columna de la izquierda tenés las ecuaciones que utilicé... si tenés dudas de por qué usé esas y no otras, podés ir acá. |
|
|
| (latm) |
ab |
bc |
cd |
da |
ciclo |
| Q |
–17,05 |
57,40 |
28,42 |
–57,40 |
11,37 |
| L |
–17,05 |
16,40 |
28,42 |
–16,40 |
11,37 |
| ΔU |
0 |
41,00 |
0 |
–41,00 |
0 |
|
|
|
a → b (isotérmica)
Qab = n R Tab ln (Vb/Va)
ΔUab= 0
b → c (isobárica)
Qbc = cp n ΔTbc
Lbc = p ΔVbc
ΔUbc = cV n ΔTbc |
c → d (isotérmica)
Qcd = n R Tcd ln (Vd/Vc)
ΔUcd = 0
d → a (isobárica)
Qda = cp n ΔTda
Lda = p ΔVda
ΔUda = cV n ΔTda |
|
|
|
| |
|
|
Te toca a vos verificar las sumas. Primero: la suma de las magnitudes de cada tramo de un ciclo es igual a la magnitud del ciclo completo (sumas horizontales). Segundo: el primer principio de la termodinámica se verifica tanto para el ciclo completo como para cada tramo de la evolución (sumas verticales). |
|
 |
| |
| |
| Desafío: Qué te puedo cobrar... |
|
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco a Joaquín Casal el envío de una errata. Última actualización nov-07. Buenos Aires, Argentina. |
|
|
| | |
|
|

