home  | más sobre termo | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
   NO ME SALEN
   (APUNTES TEÓRICOS DE BIOFÍSICA DEL CBC)
   MAQUINAS TERMICAS

 

nomesalen

 

Thermal machines

As I told you in the article about the First Law, although thermodynamics came as a scientific response to explain how the machines and engines that appear in the industrial revolution work, the principles discovered can be applied to any system, for example, mechanical systems, living systems, computer systems, electrical systems ... whatever you could think of.

However we always go back to the thermal machines, because its simplicity helps to understand the concepts born in thermodynamics.

This is the typical scheme of a thermal machine operating at a constant rate (that is, without varying its own temperature), and therefore keeping constant the internal energy, ΔU = 0.
 

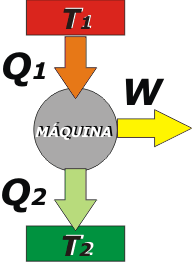The elements of the scheme are:

 

  • The hot source, here represented with a red rectangle (which could be a  boiler, or a combustion chamber or anything at high temperature). The temperature of the source is T1.
  • The cold source, here represented with a green rectangle (which could be the environment). The temperature of the cold source is T2, with T1 > T2, logically.
  • The machine itself, which usually operates cyclically, at a constant rate.
  • The three arrows are: Q1, which symbolizes the heat taken from the hot source; Q2, which is wasted heat flowing to the cold source; and W, which stands for the work done by the machine.
 
Both W and L are ways to symbolize
work

And of course, every thermal machine must fulfill the First Law of Thermodynamics:
Q1 – Q2 = W .

Thermal efficiency

The concept of efficiency in thermodynamics, η, has no different meaning from the one in colloquial language. A machine (like a business) yields the higher the benefit and the lower the cost or the investment. In the case of the machine the benefit is the work from which it is obtained. And the cost is the heat obtained from the hot source (heated with wood, petrol fuel, diesel, or anything that costs money). So the Thermal Efficiency, which is symbolized by the lowercase Greek letter, eta, η, would be...

    
  η = W /Q1 Thermal efficiency
   

If we represent the work according to the First Law...

η = (Q1 – Q2) /Q1

η = 1 – (Q2/Q1)

Then we can see that the efficiency of a thermal machine is always a number ranging from 0 to 1, closer to 1 the less the wasted energy, Q2, and the closer to 0 the greater the waste.

As is easy to deduct from the definition, efficiency is a number, so it has no units. It is customary to present it in percentage.

    

NOTE: in books, the codes, positions and subscripts for the schematic elements of the thermal machine vary widely. It is very common to use C for hot source (instead of 1) and F for cold source (instead of 2); same for the heats. The positions - up or down - of the sources also varies.
 

 
   

Curious Facts

    
  • When you learn to apply the Second Law of Thermodynamics to the operation of thermal machines, you will see that the energy and temperature rate in which they can operate is quite restricted..
  • The efficiency of a car engine with petrol fuel is around 25%; a car engine with diesel has efficiency about 35%, while electric motors are around 80%. The efficiency of the human body is close to 20%.
  • In 1822, a 26-year-old boy named Sadi Carnot realized that the efficiency of thermal machines would be maximum when the quotient of heats Q2 / Q1 was equal to the quotient of temperatures T2 / T1. What he did not realize was that -without knowing it- he was formulating the Second Law of Thermodynamics (very early).
  • There are those who think that the thermal machines are objects of museums, sympathetic devices of the past. Thermal machines almost identical to their progenitors of the old locomotives, are the ones that transform the caloric energy of the nuclear power plants to move the dynamos that generate electrical energy. The steam engine is alive!
  

Captious Questions

  
  • Could you make a scheme -like the one of the thermal machine-for the human body, and describe its parts?
  • What do you think ...Could there be a thermal machine that did not have any waste? That is, that Q2 was null? That is, efficiency equal to 1?
  
 
     
Some rights reserved. Reproduction permitted if quoting the source. Last updated on Jan-17.Translated by Esteban Djeordjian. Buenos Aires, Argentina.