NO ME SALEN
(APUNTES TEÓRICOS DE BIOFÍSICA DEL CBC)
Calorimetry, warmth, temperature
|
|

|
| |
The first thing you got to know in this chapter is that warmth and temperature -in physics – are different things. In common language, they are used almost like synonyms. But not here.
Temperature, denoted by T, is a matter manifestation which cannot be detected by the senses of our skin and – basically- by the thermometers. In case you want to inquire deeply you can go here, where I explain that temperature is about an emergent property of the average cinetic energy between every molecule and atom that integrate a body (of movement, about agitation). I won’t extend the subject because you already know perfectly what is and how to measure temperature (don’t make me lose my temper).
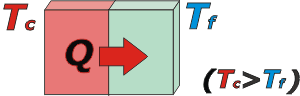
Warmth - denoted by Q- instead, is not a concept easy to measure or explain. Warmth is energy flowing from one body to another, which you notice through temperature changes or matter's state changes (e.g., from solid to liquid) or other subtler changes ... though, you'll notice: there will not be ambiguities.
The following example is quite illuminating: say two bodies get in contact: one is really hot, and the other is quite cold (namely: one is at really high temperature and the other at lower). Since they interact with each other, suddenly, the body at higher temperature “gives” warmth to the body at lower temperature, which receives it. |
| |
|
|
Remember to use T for temperature and t for time |
|
Warmth makes the “colder” body to increase his temperature. This process continues until the temperature of both bodies equals. |
|
|
Warmth always “flows” spontaneously from de body with higher temperature, to the body with lower temperature. |
|
|
|
|
Then, since warmth is energy, it can be measured in joules (denoted by J), although is really frequent to use a particular measurement unit for this kind of energy –which is also quite particular-: it’s called calorie, and is denoted cal. The equivalence between them is:
1 cal = 4,187 J
ergo:
1 J = 0,24 cal
Of course, there are other ways to transmit warmth, without having contact with a body at a higher temperature. A common example is using the stove to heat a liquid (remember, the stove must be glowing).
Warmth and temperature increase
If we transmit too many different bodies an equal amount of heat (for example, if we put every body at the same time on the stove), they will have different temperature changes.
For example, say we have a 1 litre (0.26 american gal) vessel full of water on the stove for 1 minute, or a 100 ml vessel (0,026 american gal) full of water for the same time... if I were you, I would not put my finger on the 100 ml vessel, that would hurt. It seems logic: you need more heat to get the same temperature increase in a body with greater mass.
But there is also an intrinsic property of bodies that makes them it easier or harder to heat. If during one minute, we have a vessel of one litre of water on the stove, or if we have an iron piece of 1 kg (2.2 lbs) heating at the same time and same stove ... well I would not recommend grabbing the iron piece with your hand. Both bodies have the same mass, but the iron piece increases much more their temperature compared with the water vessel. Noticeably, iron is easier to heat that water.
Every word said can be summarized in a simple expression that describes body’s temperature changes when they receive or give heat. |
|
|
|
|
|
where c is the intrinsic property of the heated material, called specific heat (also known as sensible heat) which describes how hard is to change the body’s temperature.
The following table shows specific heats of some common materials (in two different units). |
|
|
SPECIFIC HEATS |
| |
(kJ/kg.K) |
(cal/g°C) |
agua líquida |
4,169 |
0,995 |
hielo |
2,089 |
0,500 |
vapor de agua |
1,963 |
0,470 |
acero |
0,447 |
0,106 |
cobre |
0,385 |
0,092 |
aluminio |
0,898 |
0,214 |
hierro |
0,443 |
0,106 |
| plomo |
0,130 |
0,030 |
| grasa |
0,690 |
0,165 |
madera |
2,510 |
0,600 |
Note: specific heats slightly rely on the body’s temperature. The values showed at the tables are averages. For the liquid water, it is common to use the approximate value is 1 cal / g. |
|
|
|
Sometimes, this intrinsic property is attributed to the body and not to the substance from which it is made. In this case, it is called heat capacity, and it is denoted by C. If we are talking about an homogeneous body constituted by a single substance, then we have:
C = c . m
Then, the temperature variation equation is:
Q = C . (TF – T0)
Heat and state changes
Matter aggregation state changes (e.g. from solid to liquid) also are the consequence of gaining or losing heat. During a state change, temperature keeps invariant. For example, while ice melts, temperature keeps stable at 0 ºC (32 ºF). And while water boils, its temperature keeps at 100 ºC (212 ºF).
For melting more ice, you need more heat. These magnitudes are directly proportional. But with the same “amount” of heat you need to melt a piece of 1 Kg of ice (2,2 lib), you could melt like 15 Kg (33,07 lib) of lead (obviously, those materials must be at their fusion temperature: 32 ºF in the case of ice, 620,6 ºF for lead).
To sum up: the state change does not only depends on the amount of matter which is changing, but also of an intrinsic property called latent heat, denoted by L.
LF, fusion latent heat, y LV, vaporization latent heat.
Q = L . m
The following table shows some latent heats and the temperature at which state change processes occur. |
|
On those functions that rely on temperature differences, using the absolute or the relative temperature scale (K or ºC) is indistinct
On those functions that rely on temperature, you have to use the absolute scale (K).
|
|
Fusion and evaporation latent heats |
| SUSTANCIA |
T fusión (ºC) |
LF ( cal/g) |
T ebullic.(ºC) |
Lv ( cal/g) |
| agua |
0 |
80 |
100 |
540 |
| plomo |
327 |
5,5 |
1.750 |
208 |
| cobre |
1.083 |
49 |
2.600 |
1.147 |
Note: units cal/g y kcal/kg are indistinct. Instead kcal/kg = 4,187 kJ/kg |
|
|
|
Curious facts: |
|
|
- In 1761 a guy called Joseph Black (1728-1799) realized that applying heat to a piece of ice won't melt immediately. Ice absorbs some of the heat without changing its temperature. Black also observed that heating boiling water would not result in immediate evaporation. From this experiments he deduced that the heat applied to both the ice and the boiling water had to combine with the ice and water particles, becoming "latent heat". This finding was one of his greatest contribution to science. He also showed that different substances have different specific heats.
|
 |
|
|
|
- Noble gases, regardless of the substance, have two specific values: molar specific heat at constant volume (cV) and molar specific heat at constant pressure (cp). I say molar because these constants are used when the mass is expressed in mol. The value of these constants depends of how many atoms compose the gas molecule: if the gases are monatomic, or diatomic, or triatomic...
For monatomic noble gases: cV = 1,5 R y cP = 2,5 R, and for diatomic cV = 2,5 R y cP = 3,5 R,
where R is the universal gases constant.
R = 8,314 J/mol K = 0,08207 l atm/mol K
- Water is a substance with amazing and unusual properties. The fact that its vaporization latent heat is 540 cal/g was determinant for designing our fundamental refrigeration system: sweating. This process is about having over our skin a thin layer of water (sweat) only for the purpose of being evaporated. Every gram of volatilized water takes with it 540 cal... and makes us feel better. Our refrigeration system is really efficient, except on the damp days, when evaporation is harder to archive. That’s why relative humidity on the environment has and indirect effect on our wellness and health.
- Water specific heat is another of its unusual properties. Water is the “harder” material to cool or heat. That’s why the presence of water always works as a temperature stabilizer.
- Thermal equilibrium is the status of a system where every body on it has the same temperature. In this situation, there is no heat flowing on the system.
|
|
|
Tricky questions: |
|
|
- Who could have been the thermometer inventor, whom defining temperature in an operative way managed to separate the concepts of temperature and heat?
- Can gases only be heated on a constant pressure on or a constant volume?
- Why the combustion engines have a refrigeration systems based on a inner pipe with water flowing?
- Why temperature variations between day and night are approximately of 10 ºC (50ºF) in coastal areas and of 30ºC (86ºF) in desert areas?
- Why is it more dangerous to get burnt with water vapour at 100ºC that with liquid water at the same temperature?
|
|
 |
| |
|
 |
| Some rights reserved. Reproduction permitted if quoting the source. Last updated on Dec-16.Translated by Esteban Djeordjian. Buenos Aires, Argentina. |
|
|
| | |
|
|