NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
 |
EM 29) Se carga a una tensión de 40 V un capacitor de 10 microfaradios, que se conecta
después con otro igual que inicialmente estaba descargado. ¿Cuánto vale la disminución de
la energía almacenada por los capacitores entre el estado inicial (con uno solo cargado) y el
estado final con la carga repartida entre ambos?. Un milijoule (mJ) es la milésima parte de
un Joule.
a) 128 mJ b) 64 mJ c) 32 mJ
d) 16 mJ e) 8 mJ f) 4 mJ
|
|
| |
Estos ejercicios ya me cansaron. Son todos iguales. Hay dos situaciones diferentes, y una cantidad que las vincula... puede ser la carga, el potencial, la capacidad... o vaya uno a saber qué. Todo depende del proceso que el enunciado te cuente. Veamos qué nos depara éste. |
|
|
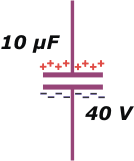 |
Voy a llamar 0 al momento anterior, y 1 al posterior. El capacitor de capacidad C0, al conectarse a una fuente de tensión V0, adquiere una carga Q0, que podemos calcular:
Q0 = C0 V0 = 10 μF . 40 V = 400 μC
Y acumula una energía, U0, que se puede calcular directamente con los datos aportados por el enunciado:
U0 = ½ C0 V0² = ½ 10 μF . 1.600 V²
U0 = 8 mJ
|
|
|
|
| Ahora viene la prestidigitación, tenés que prestar mucha atención. El enunciado dice apenas: se conecta
después con otro igual que inicialmente estaba descargado... |
|
|
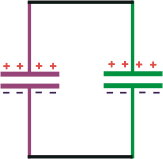 |
Pero eso significa que la carga que ya había acumulada en el capacitor... no puede escaparse, no puede cambiar. A lo sumo puede repartirse por el nuevo espacio que ahora encuentra... pero la cantidad total ha de ser la misma. O sea:
Q0 = Q1 = 400 μC
También ocurre que, siendo ambos capacitores iguales, se reparte miti-miti entre ambos. Eso se podría demostrar formalmente, pero no vale la pena, no lo vamos a necesitar. Hacélo vos, que mal no viene. |
|
|
|
| La cuestión importante es que: siempre que tengas un conjunto de capacitores, nos conviene trabajar no con el conjunto sino con el equivalente del conjunto. En este caso es muy sencillo, porque tratándose de un simple paralelo, el capacitor equivalente tendrá una capacidad que es la suma de sus componentes; o sea, el doble del original, 20 μF. |
|
|
 |
Con esta configuración sencilla podemos calcular la nueva energía acumulada:
U1 = ½ C1 V1² = ½ Q1² / C1=
U1 = ½ (400 μC)² / 20 μF
U1 = 4 mJ
|
|
|
|
Si conocemos la energía que había antes, y la que hay después, podemos conocer la variación de energía:
ΔU = U1 — U0 = 4 mJ — 8 mJ =
|
|
|
|
|
|
| |
|
 |
| Desafío: ¿Cuánto vale la diferencia de potencial en cada uno de los capacitores de la configuración final? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-08. Buenos Aires, Argentina. |
|
|
| | |
|
|

