NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
 |
EM 18) Dos condensadores, uno de 1 mF y otro de 2 mF, se conectan en paralelo a una fuente
de 1000 V. Una vez cargados se desconectan de la fuente y se conectan entre sí, uniendo
las armaduras que tienen carga de distinto signo. Entonces, cuando se alcanza el equilibrio,
la carga final de cada uno es, respectivamente
a) 333 mC y 667 mC; b) Cero y cero; c) 1000 mC y 2000 mC;
d) 667 mC y 1333 mC; e) 1000 mC y 1000 mC; f) otro valor. |
|
| |
| Acá tenés otro de esos ejercicios en los que de nada sirve cuántas fórmulas te hayas traído en el machete. Lo único que cuenta es que entiendas o no entiendas cómo se comportan las cargas, las baterías y los capacitores. La parte de los cálculos de carga en cada capacitor es tan fácil que debería hacer el relato sin explicar de dónde salen... pero vos sabrás disculpar, lo voy a hacer como para un estudiante que no lo sabe. |
|
|
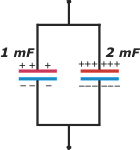 |
Este es el conjunto que fue conectado a una fuente de 1.000 V . Lógicamente, al ser un paralelo, es la misma diferencia de potencial para ambos capacitores, cuyas cargas resultan de esta sencilla operación: Q = C . ΔV
Q1μF = C1mF . ΔV = 1 mF . 1.000 V = 1 C
Q2μF = C2mF . ΔV = 2 mF . 1.000 V = 2 C
|
|
|
|
| En total tenemos 3 coulombs, repartidos 2 en el más grande y 1 en el chico, lo cual era esperable porque el grande era el doble del chico. Lo representé con carguitas (+ y -), colocando 3 pares en uno y 6 en el otro: el doble. |
|
|
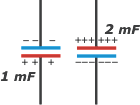 |
La cuestión es que ahora desconectamos la pila y damos vuelta uno de los capacitores -no importa cuál-: al desconectar la pila de los capacitores, éstos mantienen sus cargas, ya que no tendrían por dónde fugarse. Un capacitor cargado permanece cargado por los siglos de los siglos, hasta que lo conectemos a algo que le permita movilizar las cargas. Ese algo viene ahora: |
|
|
|
| Conectamos nuevamente para armar un nuevo paralelo. Y mirá lo que pasa: |
|
|
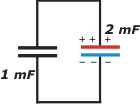 |
la conexión se establece mediante cables cuyo material conductor permite no sólo el desplazamiento de las cargas sino también la coexistencia de cargas de distinto signo, y tanto en el (cable) de arriba como en el de abajo, coexisten cargas de distinto signo. Su atracción mutua las va a atraer y se van a juntar de a pares. Cuando un par de cargas de distinto signo se juntan se neutralizan mutuamente... desaparecen. Pero acordate que dije de a pares. |
|
|
|
Eso implica que, de cada lado, sólo va a sobrevivir el exceso que no haya podido aparearse. Fijate, es sencillo: sólo queda 1 coulomb de cargas positivas en la placa que ya era positiva del capacitor grande, y 1 coulomb de cargas negativas en la placa que ya era negativa en el capacitor grande, que era el que tenía los excesos. El capacitor chico se quedó -momentáneamente- sin cargas. |
|
|
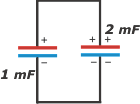 |
El coulomb de cargas (que es una bocha) que quedó en el capacitor grande está realmente cómodo, pero mucho más lo va a estar cuando se vuelva a reacomodar y ocupar el capacitor chico... que ahora está vacío. Algunas cargas irán a acomodarse allá. El reparto es predecible, porque ya lo vimos en el primer paso: en el grande quedará el doble de cargas que en el chico; o sea: 0,66 coulombs en el grande y 0,33 coulombs en el chico. ¿Cómo haría el cálculo si no fuera TAN inteligente? |
|
|
|
Recurriría a este sencillo sistema de 2 ecuaciones:
La suma de las cargas debe ser igual a la carga total: Q'1mF + Q'2mF = 1 C
La diferencia de potencial tiene que volver a ser la misma para ambos capacitores (aunque diferente de lo que era antes): ΔV'1mF = ΔV'2mF . Te lo dejo a vos. |
|
|
333 mC y 667 mC respuesta a)
|
|
|
|
| |
|
 |
| Desafío: ¿Cuánto vale la nueva diferencia de potencial? ¿Te animás a encontrar tres modos diferentes de calcularla? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-07. Buenos Aires, Argentina. |
|
|
| | |
|
|

