NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
 |
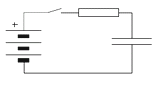
36) Se conecta una fuente de 1.000 V cc a un
capacitor de 1.000 μF inicialmente descargado, a
través de un resistor de 1.000 Ω. Cuando finalice la
carga (a) ¿cuánta energía habrá entregado la fuente
al circuito? (b) ¿cuánta habrá recibido el capacitor?
(c) ¿y cuánta habrá disipado el resistor? (sobra un
dato). |
 |
|
| |
Acá tenemos un problemita de los que llaman "tramposos", porque es recontra sencillo pero está lleno de esos pequeños detalles recontra salames que para un iniciado representan escollos recontra insalvables. Creeme, lo hacen sin mala intención. Y al final te lo voy a demostrar.
El símbolo ese raro de la izquierda no es más que el símbolo de la pila repetido verticalmente 3 veces. La palabra "pila" viene originalmente de que las primeras fuentes se construyeron armando apilamientos de monedas y trapitos mojados. Había un sanguchito básico formado por dos monedas de distinto metal (por ejemplo una de cobre y la otra de estaño) y en el medio un paño embebido en ácido. El sanguchito ese se repetía seis o siete veces y se disponían apilados verticalmente. Lo que quedaba era una pila de monedas. Entre la moneda de más abajo y la de más arriba se establecía una diferencia de potencial suficiente para divertirse por un buen rato. De ahí viene la palabra pila.
Cuando abrís un aparato cualquiera para colocarle las pilas y te encontrás que hay lugar para tres, lo más probable es que haya que colocarlas en serie (polo negativo de una pila con el positivo de la siguiente...), y si tuvieses que esquematizar el circuito la representación correcta sería como la de este ejercicio. Si cada pila tiene una diferencia de potencial de 1,5 V, el agrupamiento en serie resulta como una única fuente de 4,5 V: el triple.
En este ejercicio, si te hubiesen representado una serie de 2 o 6 o 20 pilas... era exactamente lo mismo: el dato es que la fuente entera provee 1.000 V de diferencia de potencial. |
|
|
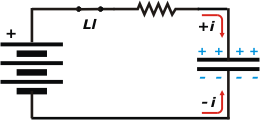 |
Pasemos a ese cosito de ahí arriba, al lado de la resistencia: se trata del símbolo para una llave, común y silvestre, como las teclas con las que se prende y se apaga la luz de la pieza. En el circuito del ejercicio está abierta (siempre hay que representarla abierta) y yo te la dibujé cerrada (sólo a los fines didácticos). |
|
|
|
Ahora sí, vamos a ver qué pasa con el ejercicio. Cuando se cierra la llave empiezan a circular cargas que salen de los polos de la fuente hacia las placas descargadas del capacitor: cargas positivas del polo positivo y cargas negativas del polo negativo (lo que ocurre en la realidad es algo ligeramente diferente; pero, como modelo de funcionamiento, la descripción que acabo de hacerte es bastante recomendable).
A medida que el capacitor se va "llenando" la corriente va disminuyendo. La cinética de llenado es típica, y te lo representé en el siguiente gráfico: |
|
|
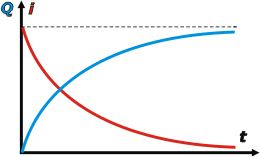 |
en celeste se grafica la carga del capacitor y en rojo la corriente (ambos en módulo). Ambas gráficas se llaman exponenciales y son asintóticas; la corriente asintótica a cero y la carga asintótica al valor de carga máxima, que para este capacitor y esta diferencia de potencial valdrá:
Q = C ΔV = 1.000 μF . 1.000 V
Q = 1 x 106 μC = 1 C |
|
|
|
Con ese dato podemos empezar a calcular las energías que nos piden. La energía entregada por la fuente, UF, es igual a la carga que entrega por la diferencia de potencial a la que la entrega.
UF = Q . ΔV = 1 C . 1.000 V = |
|
|
|
|
|
La energía almacenada en el capacitor, UC, es menor que la de la fuente, porque las primeras cargas viajan prácticamente gratis. La diferencia de potencial inicial del capacitor es cero, y no hay cargas de igual signo en cada placa taponando la entrada de las primeras que van llegando. La expresión que describe la energía almacenada en el capacitor surge de integrar el trabajo eléctrico para almacenar cada carga desde la primera a ΔV = 0 V, hasta la última, a ΔV = 1.000 V.
UC = ½ . Q . ΔV = ½ . 1 C . 1.000 V =
|
|
|
|
|
|
| ¿Y adónde fue a parar la diferencia de energía? Justamente, esa diferencia es la que se disipó en la resistencia, ER, y fue a parar al medio ambiente en forma de calor. Qué pena. |
|
|
|
|
|
El tiempo que tarda el capacitor en cargarse es típico de cada par resistencia-capacitor (RC). Y como dato curioso te agrego: si multiplicás 1 ohm por 1 faraday obtenés... ¡1 segundo! Hacé vos la prueba, vas a ver que da.
Como ves, un ejercicio como éste, charlado en clase, tiene una riqueza considerable. Y las "trampas" que vos pensaste que había no eran más que centros que la cátedra le tira a sus docentes para enriquecer las clases con un par de goles.
No me parece bien que te digan que sobra un dato, de eso ya te hablé en otro lugar, pero acá es la mejor prueba de que la intención del autor del ejercicio era mimarte y no hacerte trampa. |
|
|
| |
|
 |
| Desafío: Te propongo una investigación: ¿en qué tipo de unidades se mide el producto resistencia x capacidad? ¿qué representa el tiempo que se obtiene de multiplicar la resistencia por la capacidad? ¿Por qué se utiliza ese tiempo y no el tiempo total de "llenado"? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción bajo la solemne promesa de citar la fuente con mucho amor y cariño. Última actualización nov-07. Buenos Aires, Argentina. |
|
|
| | |
|
|

