NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
 |
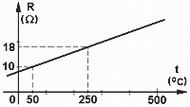
21) De acuerdo con el siguiente gráfico de resistencia en función de la temperatura,
determinar el valor de la misma a 500 ºC. |
 |
|
| |
Parece ser, según cuenta este ejercicio, que hay resistencias que varían con la temperatura. El fenómeno es absolutamente cierto y ampliamente extendido. Yo diría: casi todos los materiales aumentan su resistencia eléctrica con la temperatura. Sin embargo en todos los libros de física, y en nuestros cursos, se predica que la resistencia de un material depende de una propiedad constante (resistividad, ρ) del largo y de la sección... y nada más.
R = ρ l / S
El problema está en que si bien la resistencia aumenta con la temperatura en casi todos los casos, ese aumento no suele ser lineal (como en este ejercicio) ni menos que menos idéntico para todos los materiales. De modo que se suele indicar la resistividad de los materiales indicando a qué temperatura fue determinado, que, en general, coincide con la temperatura más frecuente en la que ese material cumple su función eléctrica.
Un modo más académico de presentar la relacion resistencia-resistividad es ésta:
R(T) = ρ l / S
que indica la dependencia no siempre lineal que te comenté.
Pero en nuestro caso se trata de una pavada: |
|
 |
| |
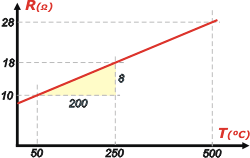 |
La función es lineal y se trata como una recta, donde la pendiente vale:
m = ΔR/ΔT
m = 8Ω / 200ºC
m = 0,04 Ω/ºC
y la ordenada al origen:
b = 10 Ω — 50ºC . 0,04 Ω/ºC
b = 8 Ω |
|
|
La ecuación de la recta queda así:
R = m T + b
R = 0,04 Ω/ºC . T + 8 Ω
Por lo tanto la resistencia a 500 ºC valdrá:
R500ºC = 0,04 (Ω/ºC) . 500 ºC + 8 Ω
|
|
|
|
| Si no te acordabas de la ecuación de la recta... no tenés que maldecir a la escuela secundaria y a la desgracia... los estudiantes siempre disponen de otros recursos. Acá te doy uno: |
|
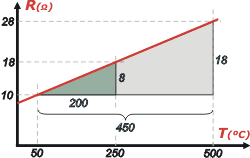 |
El triángulo grande (gris) y el chico (verde), que está superpuesto al grande, son semejantes, luego, el cociente entre sus lados es proporcional:
|
|
| Donde X te da 18, que sumados a los 10 en que están apoyados los triángulos, obtenés los mismos 28 Ω que obtuve yo de un modo más elegante. |
|
|
OBSERVACIÓN: Si tenés un multitéster (esos aparatitos que miden variables eléctricas), y medís la resistencia de una lamparita eléctrica vas a obtener un valor cercano a 50 Ω. Sin embargo la potencia impresa en el cristal de la bombita indica, por ejemplo, 100 W, lo que se corresponde con una resistencia de...
Pot = ΔV²/ R
R = ΔV²/ Pot
R = (220 V)²/100 W
R = 484 Ω
Es que, efectivamente, 484 Ω es la resistencia verdadera del filamento de la bombita... ¡cuando está encendida! y ¡caliente! No los 50 Ω que mediste vos en frío. El filamento de una lamparita suele alcanzar los 2.000 ºC sin mosquearse.
El aumento de la resistencia con la temperatura obedece a que en un material a alta temperatura sus moléculas se agitan con mayor violencia dificultando aún más el pasaje de las cargas eléctricas... ¡qué falta de cooperación, loco!
Te lo hice muy largo... así que te perdono el desafío. |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Imprimirlo en mala calidad está penado por la Ley. Idem si usás papel berreta. Última actualización oct-08. Buenos Aires, Argentina. |
|
|
| | |
|
|

