NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
 |
3) Un plano infinito se carga de manera que el campo eléctrico |E| = 2,25 103 N/C para un
punto que se halla a 3 m del plano.
a) Dibuje las líneas de campo.
b) Calcule la diferencia de potencial para dos puntos ubicados a 5 m y 7 m del plano. ¿Cambia el resultado anterior si los puntos indicados están sobre una misma línea de
campo?
c) Calcule la energía cinética que adquiere un electrón cuando se mueve desde el
reposo a lo largo de un centímetro. |
|
| |
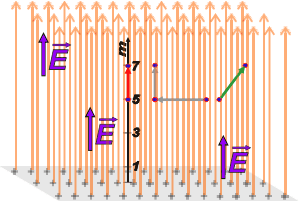
Infinito... qué palabra, tan enigmática, tan borgiana... Ahí tenés el dibujo del campo producido por una carga de distribución homogénea en un plano... infinito. Lógicamente, sólo pude dibujar una porción: el plano gris de la base, en el que se hallan las cargas sigue para acá y para allá sin encontrar nunca un borde. Y las líneas de campo, todas derechitas, paralelas y perpendiculares al plano... ¡también son infinitas de largas y se extienden hacia arriba sin alcanzar un final! (Yo tuve que cortarlas porque temía que vos no tuvieses un monitor tan alto... además aproveché para dibujarle, en el corte, una punta de flecha, que indica que las líneas de campo están orientadas). |
|
|
 |
Te imaginarás -es obvio- que tal plano y tal campo no existen en la realidad... Pero muchas veces no resulta una mala aproximación para situaciones de escala pequeña. En esos casos los físicos ahorran palabras y dicen que el plano es infinito... en el fondo, son poetas.
Ahora bien, tal como lo ves, y como podés imaginar su falta de bordes, el campo es constante y uniforme... vale siempre lo mismo y apunta siempre para el mismo lado estés donde estés, tanto a 3 m del plano como a 25. |
|
|
|
Y su valor constante en cualquier posición será la misma:
E = 2,25 x 10³ N/C
O también:
E = 2,25 x 10³ V/m
Pero no te olvides que se trata de un vector, y lo que tenés escrito ahí arriba es sólo el módulo, el valor numérico. En el dibujo lo representé tres veces: en una posición a 3 m del plano y en otras dos cualesquiera más, y siempre con un vector representativo del mismo largo, de la misma dirección y del mismo sentido... o sea, constante.
La diferencia de potencial entre dos puntos a 5 y 7 m la hallamos como el producto entre el valor del campo y la diferencia de posición:
ΔV5-7 = E . Δx
ΔV5-7 = 2,25 x 10³ V/m . 2 m
|
|
| La redacción del enunciado no es muy feliz. Lo que pide es la diferencia de potencial entre los niveles 5 y 7 metros. |
|
|
|
|
Te habrás dado cuenta que el mismo valor hubiéramos obtenido si calculábamos la diferencia de potencial entre el metro 9 y el 11. Y tampoco cambiaba la respuesta si los puntos se hallaban ubicados en posiciones laterales diferentes como las que dibujé con las frechas gris y verde. De hecho, la diferencia de potencial entre cualquier par de puntos situados a la misma distancia del plano vale cero. Esas familias de puntos entre los que la diferencia de potencial es nula forman planos que reciben el nombre de equipotenciales (tienen el mismo potencial).
La energía cinética, Uc, de un electrón (o de cualquier carga) que se mueve dentro de un campo eléctrico se puede hallar multiplicando el valor del campo, por la carga, por el desplazamiento (que en este caso es perpendicular y hacia el plano).
Uc = E . e- . Δx
Uc = 2,25 x 10³ N/C . 1,602 x 10-19 C . 0,01 m
|
|
|
|
|
|
También lo podríamos haber calculado como el producto entre la carga y la diferencia de potencial entre las dos posiciones:
ΔV1cm = E . Δx = 2,25 x 10³ V/m . 0,01 m = 22,5 V
Uc = ΔV1cm . e- = 22,5 eV
El electrón-volt, eV, es una unidad de energía muy pequeña que equivale a...
1 eV = 1,602 x 10-19 J
Así que supongo que los dos resultados son iguales, ¿te fijás? |
|
|
| |
|
 |
| Desafío: ¿Cuánto vale la velocidad de ese electrón? |
|
| |
|
Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-08. Buenos Aires, Argentina.
|
|
| | |
|
|

