NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
 |
1) Make a qualitative drawing of field lines that correspond to the following charge distributions:
a) A positive charge
b) Two positive charges of the same value, separated by a distance d
c) An electrical dipole
d) Two parallel plates uniformly charged with equal modulus and opposite sign charges. |
|
| |
OK, I’ll do them for you. You could find them in any electricity webpage searching the Internet for spectrum, electric field, whatever... I’m going to try to discuss it a little bit in each case. At the end comes the highlight. |
|
 |
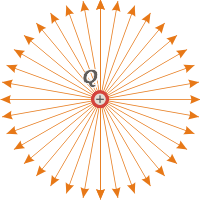 |
A positive charge. The simplest spectrum. It consists of straight field lines leaving the charge in all directions.
Don’t forget that this is a bi dimensional representation. Actually, the spectrum is tri dimensional, like a cactus.
Field lines orientation (leaving from positive charges and arriving at negative ones) is a convention. But due to this, positive charges are called sources. |
|
|
You can see that the farther away the field lines are from the source, the lower the “density per unit of area” (or volume). This line density is an indicative of electric field intensity. |
|
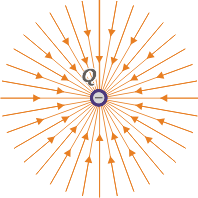 |
The electric field generated by a negative charge looks very similar to the one generated by a positive one.
The difference being the orientation of the lines field, that “enter” the charge.
This is the reason why negative charges are called “sinks”.
The place where the arrow is drawn is arbitrary and has no relevance. Field lines always start and end in an electric charge. |
|
|
Let’s look at a pair of positive charges. |
|
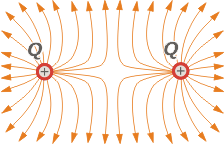 |
Pay attention to this detail: field lines never cross each other (this is true for any charges configuration, for any electrical field).
Seen from far away, the field is identical from the one created by a single lonely charge. Far away is, at least, a distance 10 times greater than the distance between the charges. |
|
|
Let’s look at a dipole, that is, a positive and a negative charge. |
|
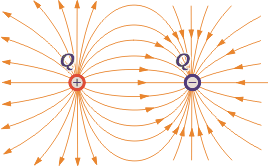 |
As you can see, lines never cross. Some are cut because of lack of space… but in theory, they are all closed, in the sense that they start in the positive charge and end in the negative one.
Seen from far away this field cancels, stops existing. Obviously, this is in practice, and let’s say that “far away” is a distance 10 times greater than the one that separates the charges. |
|
|
| Let’s look at the case of charged plates: |
|
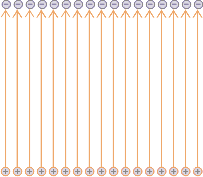 |
Undoubtedly, this is the most important because of its presence in electronics and biology.
As you can see, this is a uniform and constant field. In the representation I’ve hidden the “edge effect” because at the edges of the charged plates the field deforms curving outwards. But in almost all relevant problems (either biological or electronic) this effect does not exist or is negligible. |
|
|
In the exercises you are usually warned about his by telling you “two infinite charged plates…”.
How are field lines constructed
Very simple, I’m going to show you in the case of the dipole, but you should proceed the same way in any other configuration. |
|
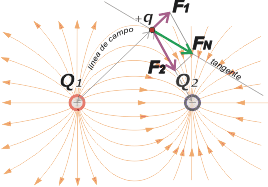 |
Place a small positive charge, +q, anywhere near the dipole. It will be subject to a repulsion force, F1, from Q1, and an attraction force, F2, from Q2. These forces do not need to be equal because neither the charges nor the distance to them have to be equal.
If two forces act on the probe charge, we can build a resultant force FN with them. The direction of this force is tangent to the field line in the position where +q is. |
|
|
| In other words: the force excerpted by a field on a charge has the same direction and sense as the electric field. |
|
| Desafío: Challenge: build a spectrum for a dipole where the positive charge is several times greater than the negative one. |
|
| |
|
| Translated by Alcides Pinto. Some Rights Reserved. Not allowed to be copied without naming either the author or this source material. Last Updated oct-11. Buenos Aires, Argentina. |
|
|
| | |
|
|