 |
NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
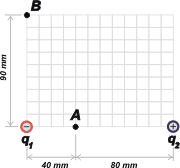
Nee 03 - Dos cargas, q1 = - 6 x 10-9 C y q2 = 6 x 10-9 C,
se hallan ubicadas en el espacio como indica la figura. Hallar el valor del campo eléctrico en los punto A y B.
Este ejercicio me lo envió gentilmente mi ex-alumno Daniel Fernández. |
 |
|
| |
Bien, se trata de campos generados por cargas puntuales. La expresión que nos permite calcular el módulo de dichos campos es:
EA1 = k q1 / dA1²
En el caso ejemplificado con los subíndices, se trataría del campo generado en el punto A por la carga 1; y es igual a la constante de Coulomb por el valor de la carga 1, y dividido por la distancia entre el punto A y la carga 1, al cuadrado.
En un ejercicio como éste, pero en el que hubiese una sola carga, conocer el valor del campo en cualquier punto en las cercanías de la carga sería una pavada. En este ejercicio, en cambio, tenemos dos cargas... no problem. El campo generado por ambas es igual a la suma (vectorial) de los campos generados por cada una por separado... que se calculan independientemente, como si la otra no existiese.
En este ejercicio en particular hallaremos dos dificultades diferentes: en el punto A se suman dos vectores campo colineales; y en el punto B sumaremos dos vectores campo no-colineales... pero no es para suicidarse. |
|
|
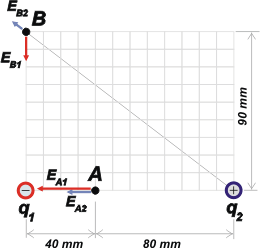 |
Acá tenemos la representación gráfica de los vectores campo, E, generados en cada punto individualmente por cada carga. Les puse un color para cada una para que te resulte más fácil identificarlos.
También marqué la distancia que hay entre la carga 2 y el punto B, que podemos hallar por pitágoras, y resulta ser igual a 150 mm (mejor aún: 0,150 m, ya que es más práctico expresar todas las distancias en metros). |
|
|
|
Procedamos con los cálculos:
EA1 = k q1 / dA1² = 9 x 109 Nm²/C² . 6 x 10-9 C / (0,04 m)² =
EA1 = 3,375 x 104 N/C
EA2 = k q2 / dA2² = 9 x 109 Nm²/C² . 6 x 10-9 C / (0,08 m)² =
EA2 = 0,844 x 104 N/C
EB1 = k q1 / dB1² = 9 x 109 Nm²/C² . 6 x 10-9 C / (0,09 m)² =
EB1 = 0,667 x 104 N/C
EB2 = k q2 / dB2² = 9 x 109 Nm²/C² . 6 x 10-9 C / (0,15 m)² =
EB2 = 0,240 x 104 N/C
Las dos primeras son las contribuciones de cada carga para generar el campo en el punto A. Hay que sumarlos para hallar el campo en A. |
|
|
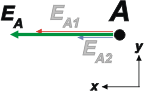 |
Aquí es muy fácil ya que ambos vectores son colineales y apuntan hacia el mismo lado.
EA = EA1 + EA2 =
EA = 3,375 x 104 N/C + 0,844 x 104 N/C =
|
|
|
|
|
EA = 4,219 x 104 N/C αA = 0º |
|
|
|
|
| Para calculaar el vector campo en B hay que hamacarse un poquito, pero si lo hacés con cuidado no tenés por qué perderte. Seguime. |
|
|
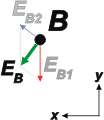 |
Primero descompongamos el vector EB2 en sus proyecciones x e y. Ese vector tiene la misma dirección que el triángulo grande en el que calculamos la distancia 2-B. Para saber el ángulo podemos aplicar el acrcotangente:
arc tg αB = Δy / Δx = 90 mm /120 mm = 0.75
αB = 37º
De modo que las proyecciones valdrán:
EB2x = EB2 . cos 37º = 0,192 x 104 N/C
EB2y = EB2 . sen 37º = 0,144 x 104 N/C
|
|
|
|
Ahora sumo los vectores de las direcciones x e y por separado.
EBx = EB2x = 0,192 x 104 N/C
EBy = EB2y — EB1 = 0,144 x 104 N/C — 0,667 x 104 N/C = — 0,523 x 104 N/C
Ahora sólo resta recomponer esas dos proyecciones (nuevamente por pitágoras) para obtener el módulo del vector campo en B. Y el ángulo que forma con el eje equis lo volvemos a sacar con el argotangente. |
|
|
|
EB = 0,557 x 104 N/C αB = — 70º |
|
|
|
|
| |
|
|
 |
| Desafío: Tratá de dibujar las líneas de campo de esta configuración en una región de 20 centímetros de radio. (Ji, ji, ji). |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción bajo la solemne promesa de citar la fuente con mucho amor, cariño, solemnidad, reverencia, circunspección e idolatría. Última actualización oct-08. Buenos Aires, Argentina. |
|
|
| | |
|
|

