 |
NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
| Nee 02) Cuatro cargas, q1, q2, q3 y q4, de -4, 8, -6 y 10 unidades de carga respectivamente, se hallan dispuestas sobre los vértices de un cuadrado de 1 unidad de longitud de lado. Hallar la fuerza eléctrica que obra sobre cada una de ellas. |
|
| |
Bien... parece tratarse de un ejercicio sencillito sobre fuerzas electrostáticas, de modo que habrá que aplicar la Ley de Coulomb:
F = k . q . q' / d²
El hecho de que no nos hayan especificado cuáles son las unidades de carga ni las de longitud (el enunciado sólo se refiere a ellas en forma genérica) lejos de constituir una complicación, resulta una facilidad. Trabajaremos todo sin unidades y nuestro resultado se obtendrá "en unidades de fuerza". Ni siquiera será necesario conocer el valor de k.
Mirá este esquema que contiene a las cargas, y a las fuerzas que recibe cada una debida a las otras: |
|
|
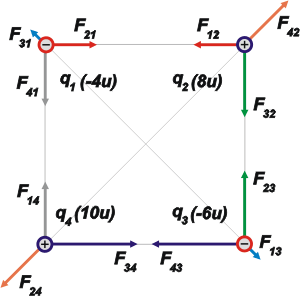 |
Las fuerzas electrostáticas (como todas las fuerzas en el universo) aparecen de a pares. Son siempre dos las cargas que se atraen o se repelen. Los pares se llaman (ya lo sabés) pares de interacción.
A cada par de interacción le puse un color diferente. Sobre cada carga deben aparecer aplicadas tres fuerzas, debido a que cada carga interactúa con las otras tres.
Cada una de las fuerzas sobre una carga le puse el nombre (con un subíndice) que indica de qué par se trata. El orden en los subíndices es convencional. Yo, para ser consistente con lo que uso en No me salen, coloco el segundo lugar de los subíndices al cuerpo que recibe la acción y en primer lugar al que la produce. |
| El esquema está hecho en escala. Los largos de los vectores que indican las fuerzas fueron tomados de los cálculos que aparecen a continuación. |
|
|
|
Aunque es más utilizada la convención simétrica, yo decidí privilegiar el orden natural en que aparece en nuestro idioma español: fuerza que X le hace a Y... Fxy.
Hallo el valor (alcanza con conocer el módulo) de cada una de las fuerzas:
F12 = F21 = k q1 q2 / d12² = 4 . 8 / 1² = k 32
F23 = F32 = k q2 q3 / d23² = 8 . 6 / 1² = k 48
F34 = F43 = k q3 q4 / d34² = 6 . 10 / 1² = k 60
F41 = F14 = k q4 q1 / d41² = 10 . 4 / 1² = k 40
F13 = F31 = k q1 q3 / d13² = 4 . 6 / 2 = k 12
F24 = F42 = k q2 q4 / d24² = 8 . 10 / 2 = k 40
Las interacciones sobre los lados del cuadrado se producen a una distancia de una unidad de longitud; y el cuadrado de 1 es 1. Las interacciones sobre la diagonal se producen a una distancia de 1,41 unidades de longitud; y el cuadrado de 1,41 es 2.
La fuerza eléctrica sobre cada carga (que es lo que nos solicita el enunciado) es la resultante entre las tres fuerzas que obran sobre cada una de ellas. En cada una habrá que realizar una sumatoria de fuerzas (en dos ejes, ya que no son co-direccionales) y así, hallar las componentes de la resultante. Voy a hacer una sola (la de la carga 2), ya que el resto sería repetitivo. |
|
|
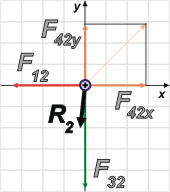 |
En este DCL ya reemplacé la fuerza F42 por sus componentes. Como esa fuerza forma un ángulo de 45º con el eje x, resulta que:
F42x = F42 . cos 45º
F42y = F42 . sen 45º
Ahora sumo por separado en cada dirección:
ΣFx = R2x = — F12 + F42x
ΣFy = R2y = — F32 + F42y
Reemplazo por los valores que calculamos antes y |
|
|
|
R2x = — k 32 + k 28,3 = — k 3,7
R2y = — k 48 + k 28,3 = — k 19,7
Para conocer el módulo de la resultante sobre la carga 2, recompongo sus proyecciones por pitágoras, y el ángulo lo calculo con el arcotangente. |
|
|
|
|
|
De igual modo resolvés las resultantes sobre las otras tres cargas. |
|
|
| |
|
|
| |
|
 |
| Desafío: ¿Cuánto vale la intensidad de de las fuerzas si el cuadrado tuviese sus aristas de longitud doble? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción bajo la solemne promesa de citar la fuente con mucho amor, cariño, solemnidad, reverencia, circunspección e idolatría. Última actualización oct-08. Buenos Aires, Argentina. |
|
|
| | |
|
|

