NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
Ned 12*) En el circuito de la figura, la corriente i vale 5 mA. a) ¿cuánto valen las corrientes i1 e i2?
b) ¿Cuál resistor disipa más potencia? |
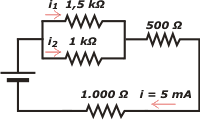 |
|
| |
Acá tenemos un ejercicio muy sencillo. Como casi siempre, para resolverlo, conviene simplificarlo con la técnica de reemplazar las asociaciones de resistencias por su resistencia equivalente. Acá es obvio que hay un lugar clave en el paralelo de las resistencias por las que circulan las corrientes que tenemos que calcular. |
|
|
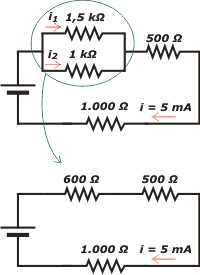 |
El valor de la resistencia equivalente del paralelo, Req, surge sencillamente de esta cuenta:
Req = (1 kΩ . 1,5 kΩ) / (1 kΩ + 1,5 kΩ)
Req = 600 Ω
El circuito equivalente que queda luego de la sustitución es tan sencillo que podemos ir resolviéndolo en el aire.
El concepto fundamental que tenemos que tener presente es que la corriente dato, la de 5 mA, pasa exactamente igual por las tres resistencias. De modo que, aplicando la Ley de Ohm, podemos calcular la diferencia de potencial a la que está sometida cada una, en especial la de 600 Ω, que es la que más nos interesa, ΔV600. |
|
|
|
Acá va:
ΔV600 = Req . i
ΔV600 = 600 Ω . 5 mA
ΔV600 = 3 V
Esa diferencia de potencial es la misma a la que están sometidas las dos resistencias originales del paralelo. De modo que si aplicamos nuevamente la Ley de Ohm para cada una obtenemos las corrientes que queríamos conocer.
i1 = ΔV600 / R1,5k
i1 = 3 V /1,5 kΩ
i1 = 2 mA
Y la otra:
i2 = ΔV600 / R1k
i2 = 3 V /1 kΩ
i2 = 3 mA
|
|
|
|
|
|
Es muy importante que repares en lo siguiente: la suma de ambas intensidades de corriente, debe -necesariamente- ser igual que la corriente que recorre al equivalente del paralelo, o sea, los 5 mA. Y es lo que nos da.
Vamos al asunto de las potencias. Calculemos las cuatro potencias.
Pot1,5k = (2 mA)2 . 1,5 kΩ = 6 mW
Pot1k = (3 mA)2 . 1 kΩ = 9 mW
Pot500 = (5 mA)2 . 500 Ω = 12,5 mW
Pot1000 = (5 mA)2 . 1.000 Ω = 25 mW
Antes de dar la respuesta podemos chequear que no hubo errores en las cuentas. La potencia total disipada entre todas las resistencias es igual a la potencia entregada por la fuente. Si calculamos las diferencias de potencial en cada resistencia podemos calcular el voltaje de la fuente:
ΔVF = ΔV600 + ΔV500 + ΔV1000
ΔVF = 3 V + 2,5 V + 5 V
ΔVF = 10,5 V
De modo que la potencia entregada valdrá:
PotF = ΔVT . i
PotF = 10,5 V . 5 mA
PotF = 52,5 mW
Si sumás las cuatro potencias, ya podés elegir la mayor, con tranquilidad: |
|
|
| |
mayor Pot = Pot1000 = 25 mW |
|
|
|
|
Es totalmente cierto que hay un modo de resolver el ejercicio más rápiro, sin tantas vueltas, casi directo. Si se te prende la lamparita podés mirar las dos resistencias por las que se divide la corriente general y razonar cómo se divide. Una resistencia es proporcional a 3/5 y la otra a 2/5. La corriente se dividirá en la misma proporción. Pero si baso toda la resolución en explicarte ese razonamiento no voy a poder enseñarte mucho. Lo de No me salen es más básico, más democrático. Cuando tengas suficiente experiencia, esos chispazos de lucidez te van a nacer espontáneamente y en un examen, corrido por el tiempo, te van a ser muy útiles y vas a poder usarlos con tranquilidad.
|
|
|
| * Este ejercicio formó parte del 2do. examen parcial de Biofísica tomado el 18 de junio de 2013. |
|
|
|
| |
|
 |
| Desafío: Sin hacer cuentas... ¿cuánto vale potencia del paralelo? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización jun-13. Buenos Aires, Argentina. |
|
|
| | |
|
|

