NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
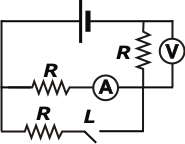
Ned 06* - Con la llave L abierta las lecturas del voltímetro y del amperímetro ideales de la figura son V y A respectivamente. Al cerrar la llave las lecturas serán:
□ 2V/3 ; A/3 □ 3V/2 ; 3A/2
□ 3V/4 ; 3A/2 □ V ; A/2
□ V/4 ; A/2 □ 4V/3 ; 2A/3 |
 |
|
| |
*Este ejercicio formó parte del examen libre de julio de 2011, y lo resolvió correctamente apenas el 5% de los estudiantes que se presentaron al examen.
Intentaré mostrarte que este ejercicio, que dejó un tendal de chiquicientos muertos, es muy simple. Para resolverlo no hay que saber demasiado de física, sólo hay que ser ordenado, saber acompañarse con muchos dibujos, y -claro está- haber hecho 18.396 ejercicios de circuitos, por lo menos.
Lo primero que tenés que entender es que el enunciado te enfrenta a dos circuitos diferentes: cuando la llave está abierta tenemos un circuito muy simple, integrado por dos resistencias iguales (ambas valen lo mismo) en serie. Acá está. |
|
|
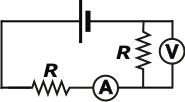 |
Como la corriente no puede pasar por la llave abierta, la resistencia de abajo queda de adorno, mejor la sacamos para que no nos distraiga.
Tal vez te cueste ver, todavía, que se trata de la más simple de las series. |
|
|
|
| Si te parece volvemos a dibujar el circuito de esta manera que es más familiar. |
|
|
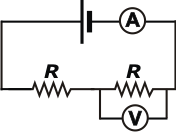 |
Por favor... antes de continuar fijate bien si el circuito que acabo de presentarte es igual al anterior. Tal vez me hagas dos objeciones.
Primero: no se trata de una simple serie de dos resistencias porque el voltímetro está conectado en paralelo a la resistencia de la derecha. Error: el voltímetro es ideal (te lo dice el enunciado) y tiene una resistencia infinita, de modo que la corriente que lo atraviesa es nula, y no hay paralelo alguno. |
|
|
|
Ese voltímetro te está indicando la diferencia de potencial a la que está sometida la resistencia cuyos extremos toca, nada más.
Segundo: este circuito tiene el amperímetro colocado en una posición diferente del anterior. Error: aunque es cierto topológicamente, no es cierto eléctricamente, ya que en una serie el orden de los elementos no altera al circuito. Además no te olvides que el amperímetro ideal tiene una resistencia igual a cero. De modo que lo coloques donde lo coloques en una serie, va a indicar la corriente que atraviesa la serie. Incluso podrías quitarlo, o colocar otros cinco, y la corriente que atraviesa la serie seguirá valiendo lo mismo. Pero siempre en serie (los amperímetros deben conectarse en serie, si no... kaput). |
|
|
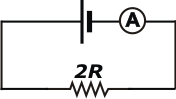 |
En definitiva, tenemos este circuito sencillísimo, que nos va a permitir conocer los valores de las indicaciones A y V, en función de las cosas que no cambian R (el valor de cada resistencia) y ΔV (la diferencia de potencial entregada por la fuente). |
|
|
|
De la Ley de Ohm:
i = ΔV / 2R
Por lo tanto, la indicación del amperímetro será:
A = ΔV / 2R
Y la indicación del voltímetro será de la mitad del voltaje de la fuente
V = ΔV / 2
Ahora veamos qué ocurre al cerrar la llave. Tenemos un nuevo circuito que es el que dibujé acá abajo. Pero lo más importante, como las indicaciones de los instrumentos son diferentes debemos cambiarle el nombre. Llamaré A' a la nueva indicación del amperímetro y V' a la del voltímetro. |
|
|
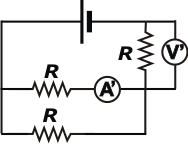 |
Lo que tenemos ahora es una serie integrada por una resistencia simple y un paralelo entre dos resistencias... todas las resistencias iguales.
Por el voltímetro no pasa corriente y el amperímetro nos marca la intensidad de corriente por una de las resistencias del paralelo. |
|
|
|
| Si te parece seguimos discutiendo el asunto con un nuevo dibujito que es equivalente al anterior: |
|
|
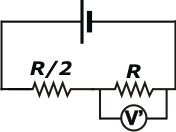 |
Lo que hice fue retirar el amperímetro, ya que no agrega resistencia, y el paralelo de las dos resistencias (dibujadas horizontalmente) las reemplacé por su equivalente: R/2.
|
|
|
|
| Hagamos un dibujito más (total a vos qué te cuesta...): |
|
|
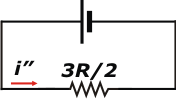 |
Ahora saco el voltímetro (total, por ahí no pasa ninguna corriente) y lo que queda es una serie entre una resistencia que vale R y la equivalente del paralelo uqe vale R/2. De modo que todo el circuito tendra una resistencia de R + R/2 = 3R/2
Eso nos va a permitir conocer el valor de la corriente que sale de la fuente en esta nueva instancia, que llamaré i". |
|
|
|
i" = ΔV / 3R/2 = 2 ΔV / 3R
Y para calcular qué diferencia de potencial marca el voltímetro, basta con multiplicar el valor de la resistencia por el valor de la corriente.
V' = i" . R = ( 2 ΔV / 3R) . R
V' = 2 ΔV / 3
Pero acordate que antes el voltímetro indicaba V = ΔV/2, de donde: ΔV = 2V. Si metemos esto en la igualdad anterior ya tendremos la segunda lectura del voltímetro en función de la primera:
V' = 2 2V / 3
V' = 4V/3
Con las opciones que nos dieron, ya hay una sola que podemos elegir. pero como nosotros somos buenos estudiantes también vamos a encontrar el valor de la nueva indicación del amperímetro, A'. Es terriblemente fácil: mirá tres dibujitos para arriba, se ve claramente que la corriente que sale de la fuente se reparte en dos caminos de igual resistencia, por lo tanto se repartirá en mitades iguales:
A' = i"/2 = (ΔV / 3R/2)/2
A' = ΔV / 3R
Ahora acordate que la primera lectura del amperímetro era: A = ΔV / 2R, de modo que ΔV = A . 2R. Si metemos eso en la última igualdad sabremos cuánto vale la nueva lectura en función de la anterior:
A' = A . 2R / 3R
A' = 2A/3
Lo sospechábamos. |
|
|
|
|
|
|
|
Bueno, espero que te haya servido de lección: no le hagas asco a hacer dibujitos, y aprendé a leer los circuitos (entenderlos aunque te los dibujen rebuscados). |
|
 |
| Desafío: Si la fuente era de 60 V y las resistencias de 3 ohm, ¿cuánto valían las lecturas de los instrumentos? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. No es recomendable meter los dedos en un enchufe mientras se toma mate dulce (¡puaj!). Última actualización jul-11. Buenos Aires, Argentina. |
|
|
| | |
|
|

