NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
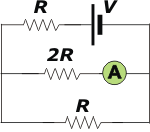
Ned 04* - La figura representa un circuito eléctrico que es alimentado por una fuente de tensión V. El amperímetro indica que por la resistencia 2R circula una intensidad de corriente I. (La fuente de tensión y el amperímetro son ideales). Entonces, la potencia que entrega la fuente es:
□ 7,5 RI² □ RI² □15 RI²
□0,5 RI² □2,25 RI² □3,25 RI² |
 |
|
| |
*Este ejercicio se tomó en el 1er. examen final de Biofísica en diciembre de 2010. Fue el ejercicio que menos aciertos tuvo (apenas un 10% de los estudiantes lo respondieron en forma correcta).
No es fácil para ningún docente deducir el motivo por el cual un ejercicio se convierte en difícil, casi irresoluble. Estimo que en este caso concurren varias dificultades que se suman. voy a ir analizándolas mientras lo resolvemos.
Sin duda, una de las dificultades estriba en que el ejercicio no tiene datos numéricos, y el circuito llama a las resistencias con los símbolos R y 2R.
Eso significa que, por ejemplo, si una de las resistencias R valiese 35 ohms, la otra resistencia R también valdría 35 ohms y la del medio, 2R, valdría el doble -o sea- 70 ohms.
Hay estudiantes que, entendiendo esto, prefieren inventar valores para las resistencia (o la magnitud que sea) como acabo de hacer yo para clarificar el concepto. Aunque no está mal hacer eso, solamente agrega complicación, y no aporta beneficio alguno. |
|
|
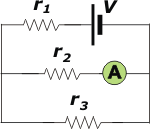 |
Otra dificultad que presenta el ejercicio es que esos símbolos con los que se han señalado las resistencias se repiten (en dos de ellas) y eso suele confundir. Un modo de salvar esa dificultad es renombrarlas con nombres únicos para cada resistencia. Por ejemplo r1, r2 y r3.
Cuando tengamos que hacer operaciones con las resistencias recordaremos que r1 y r3 tienen un valor R y que r2 tiene un valor 2R. |
|
|
|
Ahora viene otra dificultad no menos importante: entender cómo se hallan agrupadas esas tres resistencias. Es obvio que TODA la corriente que sale de la fuente está pasando por r1. (El sentido de la corriente es arbitrario, no importa si va para un lado o el otro). De modo que r1 está en serie con el resto.
También es obvio la corriente se divide en dos (partes no necesariamente iguales) y una parte pasa por r2 y el resto por r3. O sea que r2 y r3 están en paralelo.
La mención que hace el enunciado en un paréntesis acerca de que el amperímetro y la fuente son ideales indica que no tienen resistencia. El amperímetro sólo indica el valor de la corriente, y a los efectos del circuito, se lo puede ignorar. |
|
|
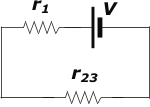 |
De modo que si simplificamos el circuito tenemos que empezar por reemplazar las resistencias r2 y r3, por su equivalente, que llamaremos r23. Incluso podemos calcular su valor.
r23 = r2 . r3 / (r2 + r3)
Reemplazando por los valores da cada resistencia:
r23 = 2R . R / (2R + R)
r23 = 2R² / 3R = 2R/3
|
|
|
|
| El circuito se puede simplificar aún más. Podemos reemplazar las resistencias r1 y r23 por su equivalente (se trata de una serie) que podemos llamar rtot, ya que es la única que queda. |
|
|
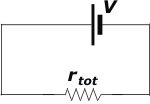 |
rtot = r1 + r23
Y también podemos hallar su valor (expresado en R).
rtot = R + 2R/3
rtot = 5R/3
|
|
|
|
| Ya avanzamos mucho. Sin embargo todavía nos falta un trecho largo para llegar al resultado. Todavía no sabemos qué corrientes atraviesan el circuito en cada rama. Pero para resolver ese asunto podemos valernos de los circuitos intermedios (equivalentes) además de la lectura del amperímetro. |
|
|
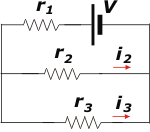 |
Las diferencias de potencial y las corrientes van a adoptar el mismo nombre que la resistencia de cada rama. Como las resistencias r2 y r3 están en paralelo las diferencias de potencial a que están sometidas son iguales, de modo que:
V2 = V3
O, lo que es lo mismo, utilizando la Ley de Ohm:
r2 . i2 = r3 . i3
|
|
|
|
El valor de i2 es el que marca el amperímetro, o sea, I. Y de las cuatro magnitudes, la única que desconocemos es i3, que podemos calcular:
i3 = r2 . i2 / r3
Reemplazando por los valores que aporta el enunciado:
i3 = 2R . I / R
i3 = 2I
Es decir que por la resistencia de abajo pasa el doble de la resistencia del medio, valga lo que valga esa corriente, que el enunciado llamó I. |
|
|
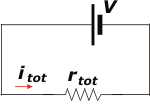 |
Para obtener el valor de la corriente que pasa por la resistencia de arriba, r1, basta con sumar las corrientes en las que se divide al abrirse en dos ramas, o sea que:
i1 = i23 = itot = i2 + i3
itot = I + 2I
itot = 3I
|
|
|
|
Recién ahora podemos calcular la potencia que entrega la fuente:
Pot = V itot = rtot . itot²
Y reemplazando por los valores que ya conocemos...
Pot = (5R/3) . (3I)²
Pot = (5R/3) . 9I²
|
|
|
|
|
|
Seguramente pensarás que la dificultad mayor se halla en lo extenso del ejercicio. Sin embargo sólo parece largo porque yo fui muy minucioso en la descripción de cada paso. Muchos de ellos se han de hacer mentalmente u obviarse cuando uno ha adquirido práctica. El circuito en cuestión es uno de los más sencillos que se puede presentar en un examen. |
|
 |
| Desafío: ¿Cuánto valen V1 y V23? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. No es recomendable meter los dedos en un enchufe mientras se toma mate amargo. Última actualización dic-10. Buenos Aires, Argentina. |
|
|
| | |
|
|

