 |
NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
| Ned 02) El circuito de la figura tiene 72 mallas idénticas (se dibujaron sólo 6, las 3 primeras y las 3 últimas, por razones de espacio). Hallar la intensidad de corriente que sale de la pila. |
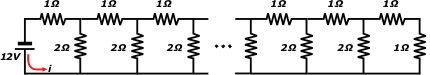 |
|
| |
Este ejercicio era un clásico de los 80. Ahora desapareció del mercado... pero a mí me encanta, y te voy a explicar por qué. Los estudiantes que no tienen método están fritos. Se quedan mirando el circuito mientras la angustia de la derrota les va carcomiendo las entrañas. Pero los estudiantes que conocen el método saben exactamente por dónde tienen que empezar. Es posible que cierta preocupación los invada, porque aún sabiendo por dónde empezar, temen que durante las operaciones que deberán hacer con esas 144 resistencias, inevitablemente, meterán la pata y errarán el resultado. No confían del todo en su capacidad de concentración ni en sus nervios de acero. Pero por lo menos no están paralizados como los otros.
Ahora... ¿qué es saber por dónde empezar? ¿Cuál es el método? Para resolver cualquier circuito siempre hay que simplificarlo reemplazando las agrupaciones de resistencias presentes por sus equivalentes, recorriendo el circuito desde lo más particular hacia lo más general. En este circuito se ve clarísimo.
Mirá, por ejemplo, las dos resistencias de 1 Ω que hay al lado de la pila... ¿está en serie o en paralelo? ¡Ni una cosa ni la otra! Serie es que: toda la corriente que pase por una debe pasar por la otra (cosa que claramente no ocurre); y paralelo es que: la corriente pasa por una o por la otra. Pero ninguna carga puede pasar por ambas (cosa que también, claramente no ocurre).
Ahora mirá la resistencia de 1 Ω que está al lado de la pila y su vecina de 2 Ω que sale hacia abajo. Nuevamente... no están ni en serie ni en paralelo... son cualquier cosa menos eso. No son nada.
Las únicas dos resistencias que están claramente, lejos de toda duda en serie o en paralelo... son las dos últimas del circuito, las dos valen 1 Ω... y no cabe la menor duda de que se hallan en serie. Es por ahí, por donde hay que empezar. |
|
|
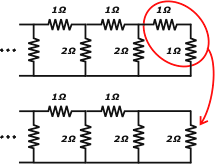 |
Y, como siempre... reemplazamos ese grupo (en este caso de dos resistencias) por su equivalente. Como se trata de una simple serie, la resistencia equivalente es la suma directa de ambas:
1 Ω + 1 Ω = 2 Ω
Ahora las saco y en su lugar pongo la equivalente a ellas que acabo de encontrar. |
|
|
|
El circuito que me queda sigue teniendo 72 mallas... pareciera que no avancé mucho. Pero ahora encuentro que en la cola de este nuevo circuito aparecen otras dos resistencias de cuyo tipo de agrupación no se puede dudar: las últimas dos resistencias, ambas de 2 Ω se hallan dispuestas claramente en paralelo. |
|
|
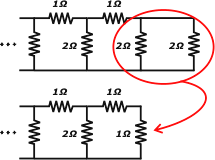 |
Por lo tanto habrá que reemplazar ese grupito de dos resistencias en paralelo por su equivalente. Para hallar ese equivalente hacemos:
(2 Ω . 2 Ω / 2 Ω + 2 Ω) = 1 Ω
Ahora las saco y en su lugar pongo la equivalente a ellas que acabo de encontrar. |
|
|
|
Nuevamente, el circuito que queda -que ya tiene una malla menos, y restan 71- tiene en la cola las únicas dos resistencias que sin ninguna duda se hallan en serie o en paralelo (los únicos tipos de agrupaciones que vos podrías reemplazar).
Pero ¡alto!, ¡no sigamos! Que esa cola es idéntica a la que teníamos en el circuito original de 72 mallas. De modo que si procedemos nuevamente como lo hicimos en los dos pasos anteriores, vamos a desembocar en una situación idéntica pero con una malla menos. No hace falta hacerlo... sabemos que iremos restando mallas y mallas (dije restando, no quitándote la malla) y al final llegaremos a la última malla, la que contiene la pila, de esta manera: |
|
|
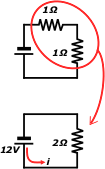 |
Y ya, recontra cancheros y con media sonrisa en los labios, reemplazaremos esas dos únicas resistencias dispuestas en serie por su equivalente, que es la equivalente total de todo el circuito:
RT = 1 Ω + 1 Ω = 2 Ω
Y recién acá -cuando hay una sola resistencia, una sola corriente y una sola fuente de potencial- nos disponemos a aplicar la Ley de Ohm para hallar la intensidad de corriente que pide el enunciado: |
|
|
|
De la Ley de Ohm, V = RT . i, despejamos la corriente:
i = V / RT = 12 V / 2 Ω
|
|
|
|
|
|
Algunos se preguntan cómo puede ser que 144 resistencias todas juntas, de 1 y 2 Ω, produzcan una resistencia de sólo 2 Ω. La respuesta es muy aleccionadora. Las agrupaciones de resistencias no siempre aumentan la resistencia total. La agrupación serie sí, siempre la aumenta, en cambio la agrupación paralelo siempre la disminuye. En el arreglo de esta malla se combina la serie y el paralelo de tal manera que se compensa el aumento con la disminución.
El ejercicio original que yo conocí se presentaba como de un largo infinito. A mí me pareció que era más distractivo y menos paralizante poner un número exageradamente grande (72) pero no imposible de abordar por estudiantes voluntariosos. |
|
|
|
|
|
| |
|
 |
| Desafío: ¿Cuánto vale la intensidad de corriente que circula por la última resistencia de 1 Ω del circuito original de 72 mallas? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción bajo la solemne promesa de citar la fuente con mucho amor, cariño, solemnidad, reverencia, circunspección e idolatría. Última actualización sep-08. Buenos Aires, Argentina. |
|
|
| | |
|
|

