NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
| Ned 1) Un bloque de cobre macizo y rectangular de 4 cm x 6 cm x 2 cm tiene entre sus caras de mayor área una diferencia de potencial que establece una corriente de 20 mA. Se lo funde y se construye otro cubito del mismo volumen, estableciendo la misma diferencia de potencial que antes entre 2 caras opuestas. ¿Cuál sería la nueva corriente? |
|
| |
Este bonito ejercicio me lo pasó Rocío Gieco, estudiante del CBC, y aunque es sencillo y reiterativo con otros ejercicios de esta guía lo tomé como modelo de una dificultad adicional -y típica- que tenía ganas de comentar acá. El ejercicio en sí mismo es una simple aplicación de la Ley de Ohm y la naturaleza resistiva de los materiales: |
|
|
| |
|
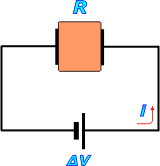 |
Se trata simplemente de aplicar la relación de diferencia de potencial, resistencia y corriente en dos circuitos sencillísimos -como el que está representado- en los que la resistencia la aporta el material conductor que el enunciado llama "cubito", pero que en realidad es un paralelepípedo rectangular (con perdón de la palabra). Esa resistencia depende en parte de la geometría del material, en particular el largo, Δx, y la sección, S.
R = ρ . Δx / S
|
|
|
|
En el primer circuito, según la descripción del enunciado, la sección vale 24 cm² (6 cm x 4 cm) y el largo 2 cm. Miralo. |
|
|
 |
De modo que la resistencia en este caso valdrá
R = ρ . 2 cm / 24 cm²
R = ρ / 12 cm
Y si con esta resistencia aplicásemos la Ley de Ohm, nos quedaría una cosa así:
ΔV = i . R
ΔV = 20 mA . ρ / 12 cm [1]
|
|
|
|
Ahora viene la parte donde se funde el "cubito" para hacer otro. La idea de "fundir y rehacer" apunta exclusivamente a plantear que tanto en el primer caso como en el segundo el material es el mismo y por lo tanto la resistividad es la misma, ya que la resistividad es una propiedad intrínseca de la materia que no depende de su cantidad ni de su geometría. El inconveniente es que también se funde la materia gris de los estudiantes.
El nuevo cubito (este sí es un cubito de verdad) tiene el mismo volumen que el anterior, supongo que no debo explicarte esa parte. |
|
|
 |
V' = V = 4 cm . 6 cm . 2 cm = 48 cm³
entonces su arista, a, será igual a la raíz cúbica de eso, o sea:
a = (48 cm³)1/3 = 3,634 cm
que no es otra cosa que el nuevo largo, Δx', que tiene que atravesar la nueva corriente. Y la nueva sección, S', será el cuadrado de eso (lado por lado). |
|
|
exponente 1/3 es lo mismo que raíz cúbica |
S' = (3,634 cm)² = 13,21 cm²
La nueva resistencia valdrá:
R' = ρ . Δx' / S'
R' = ρ . 3,634 cm / 13,21 cm²
R' = ρ / 3,634 cm
Si ahora volvemos a aplicar la Ley de Ohm nos queda:
ΔV = i' . R'
ΔV = i' . ρ / 3,634 cm [2]
La diferencia de potencial no cambió, es la misma en ambos casos (por eso no le puse la comilla), y es lo que me permite vincular las dos situaciones, [1] y [2]:
20 mA . ρ / 12 cm = i' . ρ / 3,634 cm
20 mA / 12 = i' / 3,634
|
|
|
|
|
|
El resultado es muy lógico porque, como ves, ahora la corriente debe atravesar más material (aumentó el largo) y por menos espacio (disminuyó el área), entonces el medio ofrece más resistencia y la corriente debe ser menor. |
|
|
| Desafío: Ahora lo volvemos a fundir y con el material construimos un cable cilíndrico de 3 metros de largo. ¿Cuánto valdrá la nueva corriente? |
|
 |
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Ay, ay, ah... No me salen, neuro.qi.fcen.uba.ar/ricuti, ah, ay, ooooh... Última actualización dic-07. Buenos Aires, Argentina. |
|
|
| | |
|
|

