 |
NO ME SALEN
(APUNTES TEORICOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
ELECTRODINAMICA - ASOCIACION DE RESISTENCIAS
|
|

|
| |
RESOLUCION DE CIRCUITOS
El método de resolución de circuitos que voy a presentarte acá es útil para resolver circuitos de resistencias, capacitores y lo que sea.
Resolver un circuito significa que dado un circuito eléctrico y algunas de las características eléctricas (resistencia, corriente, voltaje y/o potencia) de algunos de sus elementos, poder encontrar todas las características restantes de todos los elementos. Lo voy a desarrollar con un ejemplo en el que voy a dar los valores de las resistencias, y vamos a encontrar el resto, pero para cualquier combinación de datos/incógnitas es útil. |
| |
Los datos que voy a dar son: V = 1.000 V
R1 = 76 Ω; R2 = 60 Ω;
R3 = 10 Ω; R4 = 30 Ω
Y las incógnitas que deberemos encontrar son:
i1, V1, Pot1; i2, V2, Pot2
i3, V3, Pot3; i4, V4, Pot4
(O sea la corriente que atraviesa cada resistencia, la diferencia de potencial a la que está sometida, y la potencia que disipa). |

|
|
|
|
El método consiste en dos etapas. En la primera etapa vamos a hacer una secuencia de simplificaciones, encontrando en cada paso un circuito equivalente más sencillo (y más simpático). |
|
|
Para simplificar un circuito hacemos uso de la asociación de resistencias, calculando la resistencia equivalente de la asociación (serie o paralelo). Lo importante es elegir bien.
¿La resistencia 1 está en serie con la resistencia 3? ¿La resistencia 2 está en paralelo con la resistencia 4? ¡No! ¡Espero que al leer las preguntas te haya surgido la duda! Del único par de resistencias del que no cabe duda cuál es su asociación es el par 3 y 4, que están en serie. A ese par y sólo a ese lo reemplazamos por su resistencia equivalente.
R34 = R3 + R4
R34 = 10 Ω + 30 Ω
R34 = 40 Ω
Cada paso de simplificación debe ser modesto pero seguro. En este nuevo circuito que tenemos, el único par de resistencias que lejos de toda duda está asociado en serie o en paralelo: es la resitencia 2 y la equivalente 34, que se hallan asociadas en paralelo. La reemplazamos:
R234-1 = R2-1 + R34-1
R234-1 = (60 Ω)-1 + (40 Ω)-1
R234 = 24 Ω
Todavía falta un último paso en esta primera etapa, y en este no hay lugar a dudas: las dos resistencias que quedan están asociadas en serie. La reemplazamos.
R1234 = R1 + R234
R1234 = 76 Ω + 24 Ω
R1234 = 100 Ω
El circuito que nos quedó es equivalente al primero... pero es el más sencillo que podríamos imaginar: una sola resistencia, una sola corriente y una sola diferencia de potencial. |
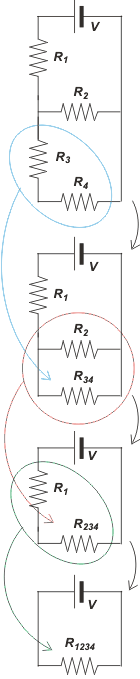 |
|
|
R1 = 76 Ω
R2 = 60 Ω
R3 = 10 Ω
R4 = 30 Ω |
R1 = 76 Ω
R2 = 60 Ω
R34 = 40 Ω |
R1 = 76 Ω
R234 = 24 Ω |
| R1234 = 100 Ω |
|
Empieza la segunda etapa: recién en este circuito podemos aplicar la ley de Ohm sin temor a equivocarnos:
V = i . R
Resolveremos este sencillo circuito, y con los resultados iremos remontando en el camino de la complejidad pasando por cada uno de los circuitos equivalentes que construímos, hasta llegar al circuito original.
No cabe duda que la diferencia de potencial a la que está sometida la resistencia 1234 es la de la fuente. La única incógnita que resta en este circuito es la corriente que atraviesa esa resistencia, que no es otra cosa que la corriente que sale de la fuente. |
|
A la resistencia equivalente de todo el circuito suele llamársela resistencia total, RT |
i1234 = V / R1234 =
i1234 = 1.000 V / 100 Ω
i1234 = 10 A
Este circuito ya está liquidado, pasemos al siguiente.
i1234 = i1 = i234 = 10 A
De cada una de esas resistencias lo único que nos falta conocer es la diferencia de potencial a la que están sometidas:
V1 = i1 . R1 = 10 A . 76 Ω = 760 V
V234 = i234 . R234 = 10 A . 24 Ω = 240 V
Cada paso que ascendemos en el retorno a la complejidad nos ofrece una oportunidad de chequear el resultado. En efecto como esas resistencias están en serie la suma de las diferencias de potencial debe ser igual a la diferencia de potencial total. Y así ocurre:
V1234 = V1 + V234 = 760 V + 240 V = 1.000 V
De este circuito no nos queda nada por averiguar. Pasemos al siguiente. En un paralelo, la diferencia de potencial de cada resistencia integrante del paralelo es igual a la diferencia de potencial de su equivalente:
V234 = V2 = V34 = 240 V
Por lo tanto, lo único que nos queda por averiguar de ese circuito es la corriente que atraviesa cada resistencia. Como siempre, para cada elemento individualmente, aplicamos la ley de Ohm:
i2 = V2 / R2 = 240 V / 60 Ω = 4 A
i34 = V34 / R34 = 240 V / 40 Ω = 6 A
Y nuestra oportunidad de chequear: la suma de las corrientes en las que se divide un paralelo es igual a la corriente que atraviesa la equivalente. Efectivamente:
i234 = i2 + i34 = 4 A + 6 A = 10 A
Ya llegamos al circuito original:
i34 = i3 = i4 = 6
Y aplicando la ley de Ohm para cada resistencia... |
 |
|
|
| R1234 = 100 Ω |
R1 = 76 Ω
R234 = 24 Ω |
R1 = 76 Ω
R2 = 60 Ω
R34 = 40 Ω |
R1 = 76 Ω
R2 = 60 Ω
R3 = 10 Ω
R4 = 30 Ω |
|
V3 = i3 . R3 = 6 A . 10 Ω = 60 V
V4 = i4 . R4 = 6 A . 30 Ω = 180 V
Y chequeamos que
V34 = V3 + V4 = 60 V + 180 V = 240 V
Si te fijás, ya encontramos el valor de casi todas las incógnitas que teníamos. Acá terminó la 2da. etapa. Pero nos faltan las potencias.
Pot1 = V1 . i1 = 760 V . 10 A = 7.600 W
Pot2 = V2 . i2 = 240 V . 4 A = 960 W
Pot3 = V3 . i3 = 60 V . 6 A = 360 W
Pot4 = V4 . i4 = 180 V . 6 A = 1.080 W
Y la potencia entregada por la fuente (le pondré subíndice F para que no se confunda):
PotF = VF . iF = 1.000 V . 10 A = 10.000 W
Y, por supuesto, tenemos nuestra oportunidad de chequear: la suma de las potencias disipadas por cada resistencia es igual a la potencia entregada por la fuente:
PotF = Pot1 + Pot2 + Pot3 + Pot4
PotF = 7.600 W + 960 W + 360 W + 1.080 W = 10.000 W
Si sos paciente y dejás la ansiedad de lado, este método resuelve todos los ejercicios. Algunas veces los datos de partida se corresponden con circuitos intermedios |
|
|
| |
|
|
CHISMES IMPORTANTES: |
|
|
- Los expertos utilizan otro método de resolución. No necesitan hacer la secuencia de simplificaciones que yo te propongo. Trabajan con el circuito original y aplican la Leyes de Kirchoff, que desembocan en un sistema de ecuaciones.
- El método también sirve para circuitos de capacitores, la diferencia es que en vez de utilizar la ley de Ohm usamos el principio de funcionamiento de los capacitores: c = Q / V
|
|
|
PREGUNTAS CAPCIOSAS: |
|
 |
- Si no era en aras de la economía y la claridad yo hubiera preferido calcular las potencias con alguna otra de las expresiones equivalentes:
Pot = V . i = i² . R = V² / R
¿Por qué?
|
|
| |
|
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Se halla altamente desaconsejado orinar en la vía electrificada de los ferrocarriles. Última actualización jun-12. Buenos Aires, Argentina. |
|
|
 |
| | |
|
|

