Este ejercicio es bastante simple, y la única lección importante que nos brinda es mostrarnos qué tipos de imágenes se obtienen al mover uno objeto delante de una lente divergente. Fijate que las distancias que nos propone el enunciado varían desde muy cerca del lente (menos de una distancia focal) hasta más de tres veces la distancia focal. Al final hacemos una síntesis (si te parece).

En los cuatro casos utilizaremos, obviamente, la fórmula de Descartes:

Y de ella despejamos la posición de la imagen, x_i:

x_i = f . x_o / (x_o – f )

y la usamos para los cuatro casos propuestos. En todos ellos la distancia focal es la misma (ya que se trata siempre de la misma lente) f = – 1 m. En el primero caso:

x₀₁ = 0,5 m

x_i1 = – 1 m . 0,5 m / (0,5 m + 1 m)

x_i1 = – 0,5 m²/ 1,5 m

En el segundo caso:

x₀₂ = 1 m

x_i2 = – 1 m . 1 m / (1 m + 1 m)

x_i2 = – 1 m²/ 2 m

En el tercer caso:

x₀₃ = 1,5 m

x_i3 = – 1 m . 1,5 m / (1,5 m + 1 m)

x_i3 = – 1,5 m²/ 2,5 m

En el cuarto caso:

x₀₄ = 3 m

x_i4 = – 1 m . 3 m / (3 m + 1 m)

x_i4 = – 3 m² / 4 m

Bueno... hagamos la síntesis. Básicamente, frente a una lente divergente se da siempre el mismo resultado: la imagen obtenida es derecha, virtual y menor. Y cuanto más alejado esté el objeto, menor es el aumento, o sea, mayor el achicamiento. A diferencia de las lentes convergentes, las divergentes hacen que los rayos no se crucen, al contrario, siempre se separan... y las cosas resultan más sencillas.

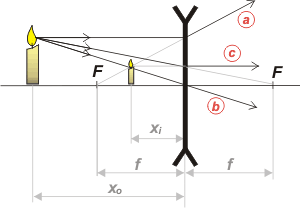Acá tenés un gráfico típico de marcha de rayos frente a una lente divergente.

a) Un rayo que llega a la lente paralelo a su eje óptico se refracta huyendo del foco.

b) un que pasa por el centro de la lente la atraviesa sin desviarse.

c) un rayo que tiene la dirección del foco sale paralelo al eje principal.

Los tres rayos que salen de la lente no se juntan... pero sus prolongaciones sí. La imagen es virtual, derecha y menor.