NMS Ad 2.2 - La velocidad media del flujo sanguíneo en una arteria de perro es 2,3 . 10^-2 m/s. ¿Cuál es la frecuencia media del sonido detectado en un aparato Döppler de medida si la frecuencia de la fuente es 10⁵ Hz (la velocidad del sonido en la sangre es 1.570 m/s)?

Doppler, Doppler... me suena... pero como que se va alejando.

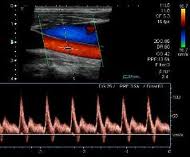
Pero no hagamos oídos sordos a este ejercicio. La técnica descripta se llama ecografía Doppler, y consiste en enviar una señal sonora (aunque 10⁵ Hz es un sonido no audible por el ser humano, ni por el perro) y registrar el rebote del sonido en un cuerpo en movimiento, en este caso la sangre. El eco llega modificado, y estudiando esa modificación puede conocerse el movimiento de la sangre.

Con la sangre alejándose de la fuente a una velocidad v, la frecuencia que la sangre recibe y que hará rebotar, f_reb, será:

f_reb = f . v_s / (v_s + v)

donde f es la fecuencia de la fuente y v_s la velocidad del sonido en la sangre. Entonces:

f_reb = 10⁵ Hz . 1.570 m/s / (1.570 m/s + 0,023 m/s )

f_reb = 99.998,53 Hz

Eso fue el camino de ida, esa es la frecuencia que recibe la sabgre y ahora es ella la que la emite y la devuelve al receptor que se encuentra en el mismo instrumento, y que recibirá una frecuencia observada, f_obs:

f_obs = f_reb . v_s / (v_s + v)

f_obs = 99.998,53 Hz . 1.570 m/s / (1.570 m/s + 0,023 m/s )

Parece muy poca diferencia... pero el instrumento es capaz de detectarla con precisión y decirnos a qué velocidad de mueve la sangre en la arteria. En el caso del ejercicio, es la pregunta contraria.

DESAFIO: integrar los dos caminos en una sola ecuación.