 |
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA Y BIOFÍSICA
Ondas, luz, óptica geométrica
|
|

|
LENTES ADOSADAS
|
|
Las lentes delgadas pueden actuar en forma conjunta. Si la distancia entre ambas es pequeña se comportan como si de una sola lente se tratase y cuya distancia focal es fácil de predecir si se conoce la distancia focal de las lentes que se adosan. Eso es lo que voy a mostrarte en esta lección.
Para demostrártelo empecemos con una sola lente cuya distancia focal es f1. Vamos a hace incidir sobre él tres rayos que llegan en forma paralela. Si la lente es convergente, los rayos deben converger a un punto que llamaré A, y que debe estar en el mismo plano focal que F1 (o sea, a una distancia f1 de la lente). |
|
|
|
|
| Los tres rayos no son tres rayos culesquiera, son tres rayos que elegí porque me convenían para esta demostración: |
|
|
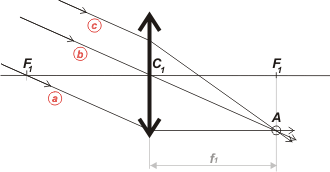 |
El rayo a que llega pasando por el foco, y que emerge de la lente paralelo al eje principal.
El rayo b que llega pasando por el centro de la lente, C1, de modo que emerge sin desviarse.
Y el rayo c que parece un rayo cualquiera pero no lo es. De todos modos no le queda más remedio que pasar por A. |
|
|
|
Ahora coloquemos cerca de la primera lente a una distancia d, otra lente, ésta otra de distancia focal f2. Los rayos ya no van a juntarse en A, pues la segunda lente los hace converger aún más y de modo que ahora habrán de cortarse en A'. Si elegimos bien los rayos, podemos localizar perfectamente la posición de A'. |
|
|
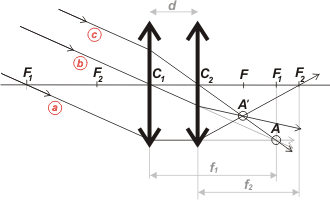 |
El rayo a que emergía paralelo ahora deberá converger pasando por F2.
El rayo c no era un rayo cualquiera, era aquel que, después de emerger de la primera lente, iba a pasar por el centro de la segunda lente, C2, y por lo tanto lo atravesaba sin desviarse. Ahí ves que se corta con el rayo a en el punto A'. |
|
|
|
Al rayo b no le queda más remedio que pasar por A', que ahora ya tenés determinado. Hagamos un poco de álgebra a ver qué nos dicen las fórmulas de Descartes si se la aplicamos a la segunda lente.
Admitamos que la imagen que produce la primera lente, A, es el objeto para la segunda. Que será un objeto negativo porque se halla delante de la lente. De modo que
xo = f1 – d.
Y la posición de la imagen, A', se halla en el plano focal del conjunto de las dos lentes, o sea F, a una distancia f de la segunda lente. Entonces: |
|
|
| |
|
|
Si admitimos que la distancia entre las lentes, d, es despreciable en comparación con sus distancias focales (o sea una lente delgada)... |
|
|
|
|
|
Resumiendo: sean f1 y f2 las distancias focales de dos lentes delgadas, no importa si son divergentes, convergentes o una y una. El conjunto de las dos lentes adosadas se comporta como una única lente cuya distancia focal llamaremos f. |
|
|
| |
|
|
| CHISMES IMPORTANTES |
|
|
-
Cuando el oftalmólogo nos prueba los lentes para decidir cuál va a recetarnos se va aproximando al valor del lente adosando dos, o tres.
|
- Si en lugar de trabajar con las distancias focales trabajamos con las potencias de las lentes (que son las inversas de las distancias focales) obtenemos que la potencia del conjunto de dos lentes adosadas es directamente la suma algebraica de las potencias de cada lente adosada. P = P1 + P2
|
|
|
 |
| PREGUNTAS CAPCIOSAS |
|
- ¿Para qué sirve adosar lentes?
|
|
| |
Algunos derechos reservados.
Se permite su reproducción citando la fuente.
Última actualización jun-10. Buenos Aires, Argentina. |
|
|
 |
 |
|
|
|

