NO ME SALEN
EJERCICIOS RESUELTOS Y APUNTES DE FÍSICA Y BIOFÍSICA DEL CBC
Cómo trazar la tengente a una circunferencia
Este ejercicio me flasheó. No sólo por su elegancia, si no por la enseñanza profunda que encierra.
Dada una circunferencia y un punto exterior a ella, trazar una de las rectas que pasan por el punto y son tangentes a ella. |
|

|
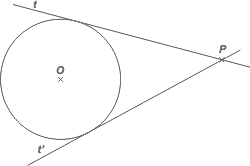 |
Aclaración: el enunciado pide por una de las rectas, ya que dados un punto (P) y una circunferencia de centro O, siempre hay dos rectas tangentes (t y t'). Bueno, ambas se hallan de la misma manera.
No cabe duda de que al iniciado la propuesta le parece una pavada atómica: bastará con tomar una regla, y buscar la recta que pase por el punto y se "apoye" en la circunferencia.
Pero las cosas no son así. |
|
|
La palabra tangente significa tocante. Alude a que toca a la circunferencia en un solo punto, punto de tangencia, que llamaremos T. (Si la tocara en dos puntos no la tocaría sino que la cortaría... sería una recta secante).
No son así porque de esa manera la recta no está determinada. Puede estar bien trazada... pero también podría estar mejor trazada. Para que la recta este perfectamente determinada hacen falta dos puntos, el punto P y el punto de tangencia, T. O sea, el método de trazado correcto consistirá en hallar T, el punto de tangencia. |
|
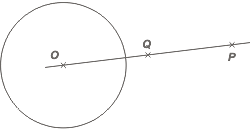 |
Se procede de esta manera: se traza la recta que pasa por P y O.
Luego se halla el punto medio del segmento PO.
A ese punto lo llamaremos Q. |
|
|
| Vamos bien... es sencillo. |
|
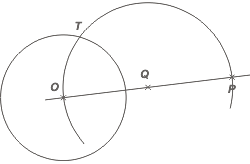 |
Ahora, con centro en Q, trazamos un arco de circunferencia que pasará por O, por P, y cortará a nuestra circunferencia en un punto, T. Que no es otro que nuestro punto de tangencia buscado. |
|
|
| Ahora sí, teniendo a P y a T, la recta tangente quedó determinada... podemos trazarla. |
|
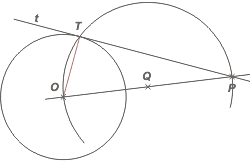 |
Y ahí está. Vamos a la justificación:
La recta tangente en el punto T debe ser normal al radio correspondiente, OT (que te tracé en rojo). Esto se debe a la propiedad de las rectas tangentes, y es obvia.
Luego, el triángulo OTP debe ser rectángulo (con su recto en T). |
|
|
| Y eso es justamente lo que se demuestra en la lección anterior, ya que el arco auxiliar que trazamos con centro en Q es un Espacio Geométrico de Tales. |
|
| Desafío: ¿Se puede hallar Q sin una regla? |
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-14. Buenos Aires, Argentina. |
|
| | | | |
| | | | |
| | | | |
|

