NO ME SALEN
EJERCICIOS RESUELTOS Y APUNTES DE FÍSICA Y BIOFÍSICA DEL CBC
|
|

|
SOLUCIONES DE LOS PROBLEMAS DE LA AUTOEVALUACIÓN
Asignate un punto por cada respuesta correcta y después analizamos el resultado final.
|
| |
|
|
PROBLEMA 1
En una reunión hay triple número de mujeres que de hombres y doble
número de niños que de hombres y mujeres juntos. ¿Cuántas mujeres, hombres y
niños hay si asistieron a la reunión 60 personas?
|
| |
Si llamo m al número de mujeres, h al de hombres, y ñ al de niños, las proposiciones del enunciado se traducen a ecuaciones así:
triple número de mujeres que de hombres → m = 3 h
doble
número de niños que de hombres y mujeres juntos → ñ = 2 (h + m)
si asistieron a la reunión 60 personas → m + h + ñ = 60
Operando con las tres ecuaciones se llega a
|
|
|
|
|
|
PROBLEMA 2
Un automóvil se desplaza a 110 kilómetros por hora. Expresar su velocidad en metros por segundo.
| | |
| Hay varios métodos para hacer pasajes de unidades (acá te los muestro); yo prefiero el que consiste en multiplicar la cantidad por cocientes iguales a uno (aquellos en los que el numerador es igual al denominador), pero no cualquier numerador ni cualquier denominador sino aquel que me va a permitir cancelar la unidad de la que quiero deshacerme y reemplazarla por la que me interesa que quede. Fijate: |
| |
110 km |
x |
1.000 m |
x |
1 h |
= |
30,56 m |
|
| |
h |
1 km |
3.600 s |
s |
|
|
|
|
|
|
|
PROBLEMA 3
Encontrar los valores de x e y que satisfacen
|
 |
200 = 24 . x + y x²
8 = 12 + y x |
|
|
|
de la segunda ecuación despejo y → y = — 4 /x
eso lo meto en la primera → 200 = 24 . x + (— 4) x |
|
|
|
|
|
PROBLEMA 4
Encontrar los valores de x e y que satisfacen
|
 |
y = 9 . x
—1,25 = 12 . x — 5 . x² |
|
|
|
Igualo la segunda ecuación a 0 → 0 = 1,25 + 12 . x — 5 . x²
Se trata de un polinomio de segundo grado donde los coeficientes son
|
|
a= — 5; b = 12 ; y c = 1,25 → se resuelve con la famosa |
| |
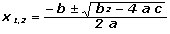 |
→ va a tener dos resultados |
x1 = 2,5 y x2 = — 0,1
con esos dos valores, por separado, voy a la primera ecuación
y1 = 22,5 e y2 = — 0,9
|
|
|
|
| |
Par 1( 2,5 ; 22,5). Par 2 (— 0,1 ; — 0,9) |
|
|
|
|
PROBLEMA 5
Las rectas de igual color son perpendiculares entre sí. Dado el valor de α = 42º , hallar el valor de β y γ. |
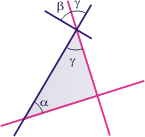 |
| Hay muchas maneras de encontrar esos valores. Te doy una: si observás detenidamente el triángulo que sombreé verás que el opuesto por el vértice de γ debe ser igual a 180º — 90º — 42º = 48º, porque la suma de los ángulos interiores de cualquier triángulo siempre da 180º. De modo que β valdrá lo mismo que α. |
|
|
|
|
|
|
PROBLEMA 6
Por un reproductor de DVD comprado en una liquidación con el 20% de descuento sobre el precio de lista se pagaron $350.- ¿Cuál era el precio de lista?
El precio de lista, L, es tal que si lo multiplicamos por 0,8 (la parte que queda por pagar después de descontar 0,2 -es decir el 20%-) da $350.- Por lo tanto L se obtiene dividiendo $350.- por 0,8 |
|
|
| |
|
|
PROBLEMA 7
α = 32º es el ángulo de un sector circular de radio
r = 53 cm. Y β es un ángulo recto. Hallar la longitud del segmento d. |
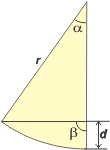 |
| Al dividir el sector circular con el segmento horizontal, la parte superior se convierte en un triángulo rectángulo, cuyo lado vertical vale r cos α. A nosotros nos interesa el segmento vertical de ahí abajo, que completa el radio, de modo que d = r (1 — cos α). |
|
|
|
|
|
|
PROBLEMA 8
Reducir esta expresión a una única fracción y simplificarla |
| |
2 x + 3 |
— |
4 x — 7 |
= |
(6 x + 9) — (8x — 14) |
= |
|
| |
6 |
9 |
18 |
|
|
|
|
|
|
|
PROBLEMA 9
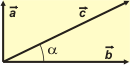
Dados los vectores a y b, que son ortogonales entre sí, y miden 7,5 y 12,5 metros respectivamente, hallar el módulo del vector c y el ángulo que forma con el b. |
 |
|
|
|
| Por el teorema de Pitágoras: c² = a² + b² , luego se aplica raíz cuadrada a ese resultado. α es el ángulo cuya tg vale a/b, luego |
|
|
| |
|
|
PROBLEMA 10
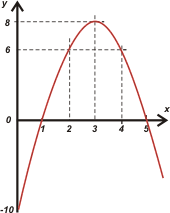
Graficar la función
y = 6 + 4 (x – 2) — 2 (x – 2)²
e indicar los valores de todos los puntos notables.
Se llaman puntos notables a máximos, mínimos, inflexión, ceros, etcétera. |
 |
| |
(0;-10), (1;0), (3;8), (5;0) |
|
|
|
|
|
PROBLEMA 11
Una canilla llena completamente una pileta en 2 horas y 40 minutos. Otra canilla lo hace en 4 horas. ¿Cuánto tardarán en llenarla las dos canillas juntas?
Definamos velocidad de llenado, V, como lleno total, Ll, dividido el tiempo total de llenado. Entonces,
canilla 1: V1 = Ll / 2,67; canilla 2: V2 = Ll / 4; ambas canillas: V1+ V2 = Ll / 1,60 (es una suma de fracciones). |
|
|
| |
T(2 canillas) = 1,60 h = 1 h 36 min |
|
|
|
|
PROBLEMA 12
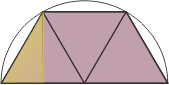
Hallar el valor del área sombreada, que está formada por tres triángulos equiláteros, y que están inscriptos en una semicircunferencia cuya longitud vale 20 m. |
 |
|
|
|
La longitud de una semicircunferencia es 3,14 por R (donde R es el radio de la circunferencia correspondiente) de modo que R = 6,37 m. Los triángulos equiláteros tienen sus 3 lados iguales, que en este caso son iguales a R. De modo que la altura, h, de uno de ellos (marcado en amarillo en un medio triángulo, que es rectángulo) se puede calcular por Pitágoras ya que la hipotenusa vale R y la base R/2. Haciendo el cálculo resulta h = 5,52 m. El área sombreada es un trapecio y su área se calcula base media por altura, A = (R+2R) . h / 2 |
|
|
|
|
|
| ¿Y? ¿Cuánto sacaste? Veamos qué hacer en cada caso. |
| |
|

