 |
NO ME SALEN
EJERCICIOS RESUELTOS Y APUNTES DE FÍSICA Y BIOFÍSICA DEL CBC
MISCELANEA DE EJERCICIOS
|
|

|
| |
| |
|
EJERCICIO 4 - Un helicóptero vuela entre dos ciudades distantes 20 kilómetros. En cierto instante se lo ve desde ambas ciudades. Desde una de ellas con un ángulo de 26 grados sobre el horizonte y desde la otra con un ángulo de 14 grados también sobre el horizonte. Hallar la distancia del helicóptero a las ciudades y la altura a la que se encuentra.
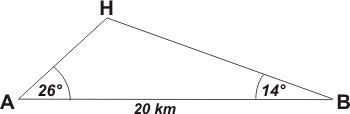
Hagamos un esquema de la situación y pongámosle nombre a los elementos del ejercicio.
|
|
 |
|
|
Supongamos que A es la ciudad que ve el helicóptero con un ángulo de 26° y B la otra. H es la posición del helicóptero. Entonces AH y BH son dos de nuestras incógnitas.
Está claro que lo que enfrentamos es un simple ejercicio de resolución de triángulos, ¿no? Te propongo que averigües el valor del ángulo en el vértice H. Coincidirás conmigo en que vale 140°, porque la suma de los triángulos interiores de cualquier triángulo siempre vale 180°.
Entonces la solución del problema es sencillísima aplicando el teorema del seno, que decía que en cualquier triángulo el seno de un ángulo dividido su lado opuesto es igual al seño de cualquiera de los otros ángulos divididos respectivamente por su lado opuesto. O sea: |
|
|
| |
sen 140° |
= |
sen 26° |
= |
sen 14° |
|
|
|
|
|
| 20 km |
BH |
AH |
|
|
|
De ahí despejamos nuestras incógnitas y las calculamos: |
|
|
| |
BH = |
20 km . sen 26° |
= |
20 km . 0,4384 |
|
|
|
| sen 140° |
0,6428 |
|
|
|
| |
AH = |
20 km . sen 14° |
= |
20 km . 0,2419 |
|
|
|
| sen 140° |
0,6428 |
|
|
|
| |
BH = 13,64 km AH = 7,53 km |
|
|
|
|
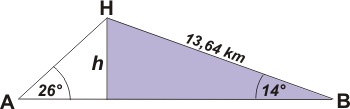
| Resultados que parecen razonables (acordate que la suma de los lados cualesquiera de un triángulo debe ser mayor que el otro lado). Todavía nos falta la altura del helicóptero. Completemos nuestro esquema: |
|
|
 |
|
|
h es la altura a la que se encuentra el helicóptero y fijate que podemos dividir nuestro triángulo original en dos triánguos rectángulos (yo pinté el de la derecha). Luego, podemos volver a aplicar el teorema del seno para este nuevo triángulo: |
|
|
| |
h = |
13,64 km . sen 14° |
= |
13,64 km . 0,2419 |
|
|
|
| sen 90° |
1 |
|
|
|
De donde: |
|
|
|
|
|
Si en lugar de usar el triángulo de la derecha hubiésemos usado el de la izquierda, por supuesto, la altura nos tendría que dar lo mismo... ¿no? Bueno, hacelo.
|
|
|
 |
|
La idea principal de este ejercicio es mostrarte cuán fácil se hace la resolución de triángulos si tenés a mano el olvidado teorema del seno. Está claro que hay varias formas más, diferentes, de resolverlo, pero ninguna tan directa como ésta. Igualmente te invito a que pruebes otros caminos. |
|
|
|
DESAFIO: También podrían interesarnos las distancias entre las ciudades y la posición horizontal del helicóptero. ¿Te animás a encontrarlas? ¿Cuál será la verificación inmediata de esos resultados? |
|
 |
| Algunos derechos reservados. Algunos izquierdos también. O sea: propiedad intelectual, propiedad vertical, propiedad horizontal y la propiedad del prójimo. Se permite su reproducción citando la fuente, o sea a mí. Última actualización feb-17. Buenos Aires, Argentina. |
|
|
|

