 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Magnitudes y unidades
|
|

|
| |
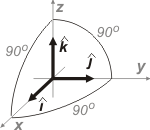
FIS v.13- Sean î , ĵ , k , los versores asociados con
las direcciones de los ejes cartesianos de la terna
derecha del recuadro gris intitulado “Versor”.
î = (1; 0; 0) ; ĵ = (0; 1; 0) ; k = (0; 0; 1)
Calcular:
a) î • î , î • ĵ , î • k
b) ĵ • î , ĵ • ĵ , ĵ • k
c) k • î , k • ĵ , k • k |
 |
|
| |
NOTA: en html, el lenguaje de internet no tenemos el tipo k con sombrerito, lo siento. |
|
|
¡Chino básico! ¡¿Qué nos están pidiendo?! Que no cunda el pánico... parece chino porque hay nueve preguntas todas juntas... pero no temas, es todo mecánico y sencillo. Lo importante son las conclusiones que vamos a sacar.
Lo que tenemos que hacer es multiplicar dos vectores, nada más. Recordarás que hay dos maneras de multiplicar vectores: el escalar (cuyo resultado es un escalar) y el vectorial (cuyo resultado es un vector). En este caso nos piden el producto escalar, cuya definición es: A • B = |A| . |B| cos θ, donde θ es el ángulo entre A y B.
î • î = 1 . 1 . cos 0°
î • î = 1
Vamos con el siguiente:
î • ĵ = 1 . 1 . cos 90°
î • ĵ = 0
Si tu hipocampo funciona bien, te podés dar cuenta que con estos dos resultados ya hicimos todo el ejercicio, por una cuestión de simetrías. El producto escalar de un versor por sí mismo es igual a uno; y el producto escalar entre dos versores ortogonales es nulo. Pero bueno... sigamos:
î • k = 1 . 1 . cos 90°
î • k = 0
|
|
|
| |
î • î = 1 , î • ĵ = 0 , î • k = 0 |
a) |
|
|
|
También podríamos plantearlo utiizando la fórmula de resolución de productos escalares que es la siguiente:
A = (xA; yA; zA)
B = (xB; yB ;zB)
A • B = (xA . xB + yA . yB + zA . zB)
Nuestro trabajo va a ser muy sencillo, porque las coordenadas de los versores valen uno o cero. Vamos con fe.
î • î = (1; 0; 0) • (1; 0; 0)
î • î = (1.1) + (0.0) + (0.0)
î • î = 1
Vamos con el siguiente:
î • ĵ = (1; 0; 0) • (0; 1; 0)
î • ĵ = (1.0) + (0.1) + (0.0)
î • ĵ = 0
Y el tercero:
î • k = (1; 0; 0) • (0; 1; 0)
î • k = (1.0) + (0.0) + (0.1)
î • k = 0
|
|
|
| |
î • î = 1 , î • ĵ = 0 , î • k = 0 |
a) |
|
|
|
El resto es todo igual. Pero si estás aburrido...
ĵ • î = (0; 1; 0) • (1; 0; 0)
ĵ • î = (0.1) + (1.0) + (0.0)
ĵ • î = 0
Vamos con el siguiente:
ĵ • ĵ = (0; 1; 0) • (0; 1; 0)
ĵ • ĵ = (0.0) + (1.1) + (0.0)
ĵ • ĵ = 1
Y el tercero:
ĵ • k = (0; 1; 0) • (0; 1; 0)
ĵ • k = (0.0) + (1.0) + (0.1)
ĵ • k = 0
|
|
|
| |
ĵ • î = 0 , ĵ • ĵ = 1 , ĵ • k = 0 |
b) |
|
|
|
Y dale...
k • î = (0; 0; 1) • (1; 0; 0)
k • î = (0.1) + (0.0) + (1.0)
k • î = 0
Vamos con el siguiente:
k • ĵ = (0; 0; 1) • (0; 1; 0)
k • ĵ = (0.0) + (0.1) + (1.0)
k • ĵ = 0
Y el tercero:
k • k = (0; 0; 1) • (0; 0; 1)
k • k = (0.0) + (0.0) + (1.1)
k • k = 1
|
|
|
| |
k • î = 0 , k • ĵ = 0 , k • k = 1 |
c) |
|
|
|
| Lo interesante se este resultado es que podemos extenderlo parcialmente a cualquier vector: siempre que multiplicas escalarmente dos vectores ortogonales el resultado es nulo, y siempre que multiplicás dos vectores paralelos el resultado es el producto entre sus módulos (si son contrarios el resultado lleva signo menos). |
|
|
Desafío: |
|
 |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| | |
|
|

