 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Magnitudes y unidades
|
|

|
| |
FIS v.09- Hallar el vector que tiene origen en el punto
A y extremo en el punto B:
a) A = (2; –1) y B = (–5; –2).
b) A = (2; –5; 8) y B = (–4; –3; 2).
|
| |
Bueno, este ejercicio viene con sorpresita. Vamos con el primero y arranquemos por graficar los puntos A y B. |
|
|
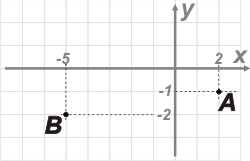 |
Esos puntos bien podrían representarse con vectores. En ese caso a esos vectores los llamaríamos vectores posición. |
|
|
|
| Ahora grafiquemos el vector que nos indica el enunciado: |
|
|
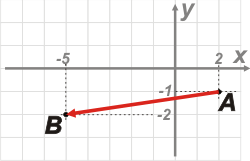 |
Ahí está. Pero todos nos imaginamos que el enunciado pretende que lo hallemos analíticamente, no solo gráficamente. ¿Cómo lo hacemos?
Muy fácil, y el gráfico nos aclara el camino. Llamemos Ra (por resta) a nuestro vector. Sus componentes serán: |
|
|
|
xR = xB — xA = — 5 — 2 = — 7
yR = yB — yA = — 2 — (— 1) = — 1
De modo que: |
|
|
|
|
|
| Si lo representamos en el mismo gráfico de los puntos mirá lo que pasa: |
|
|
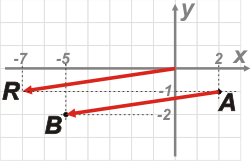 |
Aparece el mismo vector que une los puntos A y B, pero centrado en los ejes de referencia.
De hecho, todos los vectores que tengan el mismo módulo, la misma dirección y el mismo sentido serán indistinguibles cuando los grafiquemos... es más serán el mismo vector. |
|
|
|
Hay fenómenos físicos en los que la posición d un vector es relevante, y ya buscaremos la forma de advertirlo cuando sea necesario. pero en otras muchísimas oportunidades esta enorme identidad entre todos los vectores de igual módulo, dirección y sentido no afecta para nada. Pero miremos otra propiedad más que nos permite ver este ejercicio.
Rerpresentemos los puntos A y B con sus vectores posición A y B. |
|
|
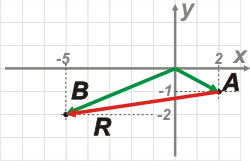 |
¿Te das cuenta? Ra (por eso elegí ese nombre) era la resta entre los vetores posición que representan los puntos A y B.
Podríamos escribir:
Ra = ΔAB = B — A
|
|
|
|
La sorpresita es que el ítem b) nos pide hacer lo mismo pero con dos puntos ubicados en un espacio tridimensional (como en el que nos parece vivir todos los días). No hay drama... operamos de la misma manera. Los punto A y B tienen tres coordenadas (no te los voy a representar, aunque no es muy difícil). Otro día vengo y lo hago.
A = (2; –5; 8) y B = (–4; –3; 2)
Entonces:
xR = xB — xA = — 4 — 2 = — 6
yR = yB — yA = — 3 — (— 5) = 2
zR = zB — zA = 2 — 8 = — 6
Luego, el vector que un A con B será: |
|
|
|
|
|
| Hagamos la representación gráfica. |
|
|
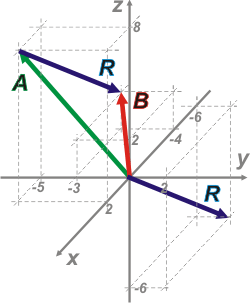 |
Representa vectores en 3 dimensiones nos obliga a utilizar perspectivas. No es sencillo ni inmediato interpretar ni -menos que menos- hacer las representaciones. Hay que adquirir cierta práctica.
Lo prmero es dibujar la terna de ejes y elegir las escalas.
Luego se marcan las coordenadas de un vector y por esos puntos se trazan paralelas a los ejes. Por las intersecciones de esas paralelas se vuelven a trazar más paralelas a los ejes... de ese modo quedan representados paralelepídedos (como ladrillos). Los vectores A y B tienen origen en el origen de coordenadas y extremo en el vértice opuesto del paralelepípedo.
El vector resta, Rb lo podés trazar uniendo los puntos A y B, o también trasladarlo al origen de coordenadas. |
|
|
|
| y ahí verificás que se trata del mismo vector, o sea, que representaste (y operaste) correctamente. |
|
|
Desafío: Escribir los vectores Ra y Rb en forma cartesiana. |
|
 |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| | |
|
|

