home  | más de hidrostática | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
   NO ME SALEN
   EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
   FLUIDOS - PRINCIPIO DE ARQUÍMEDES		  

desesperado

 
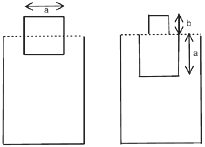
FIS H.21) En la figura un cubo de arista 1 cm y densidad ρc flota en un líquido de densidad 1.4 g/cm³, de modo que está sumergido hasta la mitad de su volumen. Otro cubo de igual densidad que el primero se apoya sobre éste y se observa que se sumerge al ras del líquido, es decir su cara superior queda en la superficie de separación aire líquido como indica la figura.
Bajo estas condiciones, hallar:
    a) ρc
    b) La arista b del bloque superior.		 Fluídos - Ricardo Cabrera

Que no cunda el pánico. Claramente hay dos situaciones diferentes, la primera es bien sencillita, en la segunda hay dos cuerpos flotando de modo poco ortodoxo (quizá hasta un poco chancho). Vamos por partes.

Primera situación (no voy a hacer esquema, arreglate con la imaginación). Sobre el cubo grande actúan dos fuerzas: el peso del cubo grande, Pa, y el empuje que recibe en esta primera instancia, E1. Como flota en equilibrio:

  

 

 

 

 

 

E1 = Pa

 [1]
   
Según Arquímedes (y me temo que a esta altura del partido hay que creerle):    

E1 = ρlíq . g . ½ Va

 [2]
   
Donde Va es el volumen del cubo grande, que vale a3 = 1 cm3. Y ½ Va  es la parte que desaloja de líquido. Por otro lado el peso de ese cubo se puede expresar como:    

Pa = ρC . g . Va

 [3]
   

Ahora vamos a la segunda situación de flotación que es un poco más compleja, pero no tanto como para que no pueda pedir que sigas usando la imaginación y no tener que hacerte un dibujito.

Sobre el cubito de arriba acúan sólo dos fuerzas: su propio peso, Pb, y el apoyo que le presta el cubo grande, N. Y está en equilibrio:

  
No me digas que no te saca de quicio que yo siga escribiendo ecuaciones...
¡y no calcule numérica-
mente NADA!

N = Pb 

 [4]
   
El peso del cubo se puede expresar así:    

Pb = ρC . g . Vb

 [5]
   
Donde Vb es el volumen del cubo chico, que vale b3, donde b es la arista de ese segundo cubo. Veamos qué ocurre ahora con el cubo grande. Las fuerzas que sobre él actúan son otras: su propio peso, Pa (que no ha cambiado), el empuje, E2, que sí cambió, porque ahora desplaza más líquido, y la fuerza con que lo aplasta el cubito de arriba y que ya tiene nombre, N. Como está en equilibrio:    

E2 = Pa + N

 [6]
   
Por último, ese nuevo empuje valdrá:    

E2 = ρlíq . g . Va

 [7]
   

Eso es todo. El resto es álgebra de sexto grado de escuela primaria. Si seguís leyendo es porque tenés un aburrimiento descomunal.

Igualo la [2] y la [3] según me lo recomienda la [1]. Y despejo

ρC . g . Va = ρlíq . g . ½ Va

ρC = ½ ρlíq

    

 

 ρC = 0,7 g/cm3  
   

Ahora, de la [7] tengo E2. Con la [3] saco Pa, y con la [6] obtengo N, que según [4] es lo mismo que Pb. De ahí me voy a la [5] y calculo Vb. A ese valor le tomo la raíz cúbica y obtengo:

    

 

 b = 1 cm  
 

 
O sea, resultó que el cubo de arriba tenía que tener el mismo tamaño que el de abajo. Ahora que si lo pienso un poquito... ¡era previsible!    
DESAFÍO: Ahora que sé que los cubos son idénticos... ¿cuántos quedarán sumergidos y cuántos en el aire si coloco una pila de 6? ¡Eureka!   Fluídos - Ricardo Cabrera
Algunos derechos reservados. Se permite su reproducción citando la fuente legítima, o sea, este sitio. Agradezco a Johanna Di Francesco por el envío de una errata. Última actualización jun-11. Buenos Aires, Argentina.