NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
FLUIDOS - PRINCIPIO DE ARQUÍMEDES |
|

|
| |
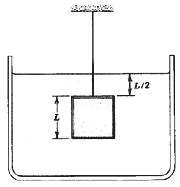
FIS H.15)* Un objeto cúbico de dimensión L= 0,6 m de lado y cuyo peso de
4.450 N está suspendido mediante un alambre en un tanque abierto
(Patm = 1 atm) que contiene un líquido de densidad ρ = 944 kg/m³.
Encuentre:
a) La fuerza total ejercida por el líquido y por la atmósfera
sobre la parte superior del objeto.
b) La fuerza total hacia arriba en la base del objeto.
c) La tensión en el alambre.
d) El empuje sobre el cuerpo. |
 |
|
OK, esto es lo que se llama un ejercicio pautado. Tenemos que encontrar un montón de cosas que no sabemos para qué sirven... lo más importante será si al final le encontramos un sentido general. Veamos.
a) La fuerza total ejercida por el líquido y por la atmósfera es una pregunta que no tiene sentido. Sobre la cara superior del cubo está en contacto el líquido y el cable, pero no la atmósfera, de modo que la atmósfera no hace ninguna fuerza sobre el cubo. Lo que el autor del ejercicio quiso decir es que calcules la fuerza del líquido utilizando la presión absoluta (o barométrica). Hacer lo opuesto (usar la presión relativa o manométrica) sería mentiroso para responder la pregunta, porque como la escala de presiones manométricas considera el cero de la escala en la superficie de la Tierra, sería como suponer que el líquido no esta presionado por la atmósfera, lo cual no es cierto. Dicho esto, vamos a los bifes:
Dentro del líquido la presión a 0,3 m de profundidad vale, según el Principio General de la Hidrostática:
Δpr = γlíq . Δh
pr0,3 = pr0 + γlíq . Δh
Y la fuerza sobre la cara superior (que se halla toda a la misma profundidad, por lo tanto a la misma presión) será:
Fsup = pr0,3 . Asup
Fsup = ( pr0 + γlíq . Δhsup ) . Asup
Fsup = (101.300 Pa + 9.440 N/m3 . 0,3 m ) . (0,6 m)2
Fsup = 104.132 N/m2 . 0,36 m2
|
|
acordate que peso específico es igual a densidad por gravedad
γ = ρ g
también acordate que presión es el cociente entre la fuerza y el área
Pr = F / A |
|
|
|
b) Del mismo modo se calcula la fuerza en la cara inferior.
Finf = (pr0 + γH2O . Δhinf ) . Ainf
Finf = (101.300 Pa + 9.440 N/m3. 0,9 m ) . (0,6 m)2
Finf = 109.796 N/m2 . 0,36 m2
|
|
|
|
|
|
c) El cálculo de la tensión, T, podemos hacerlo desde dos planteos diferentes. Siguiendo la pauta del ejercicio, si las fuerzas que recibe el cubo en sus caras laterales se cancelan entre sí (ya que la fuerza sobre una cara debe ser igual y opuesta a la de la cara opuesta) entonces la tensión viene a compensar la diferencia de fuerzas entre las caras superior e inferior y el peso del cubo, P. La suma de fuerzas lo diría de esta manera:
T + Finf = Fsup+ P
T = Fsup — Finf + P
T = 37.488 N — 39.527 N + 4.450 N
|
|
|
|
|
|
d) El empuje, E, podemos calcularlo según el Principio de Arquímedes, o sea, calculando el peso del líquido desalojado en un volumen igual al del cubo.
E = γlíq . V
E = 9.440 N/m3 . (0,6 m)3
|
|
|
|
|
|
Acá viene el sentido general. El empuje no es otra cosa que la fuerza neta entre las fuerzas que empujan para abajo (la de la cara superior) y las que empujan hacia arriba (la de la cara inferior).
E = 39.527 N — 37.488 N = 2.039 N
Justamente así es como se demuestra el principio de Arquímedes, utilizando un cuerpo de geometría simple, como un cubo o un cilindro. Pero lo fecundo del concepto de empuje es que se puede extrapolar a cualquier cuerpo, cualquiera sea su forma y tamaño. |
|
|
| |
|
|
| DESAFÍO: ¿Cómo podemos asegurar que las fuerzas laterales en caras opuestas son iguales? ¿Cómo podríamos calcularlas? |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente legítima, o sea, este sitio. Agradezco a Gabriela Velarde por el envío de una errata. Última actualización
jun-11. Buenos Aires, Argentina. |
|
|
| | |
|
|

