 |
NO ME SALEN
(PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC)
FLUIDOS
|
|

|
| |
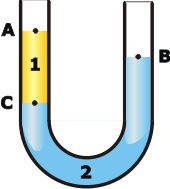
NMS 33* - En un tubo en U como el de la figura, se colocan dos líquidos inmiscibles de densidades ρ1 = 1,2 g/cm³ y ρ2 = 2,6 g/cm³.
a) Ambas ramas se encuentran abiertas a la atmósfera, donde la presión es 101.325 Pa, y cuando se alcanza el equilibrio, el punto A se encuentra 0,5 m por encima del punto B. Calcule la altura de la columna 1.
b) En cierto instante se cierra a rama derecha, encerrando un gas sobre el líquido 2. Si la rama izquierda sigue abierta a la atmósfera, se alcanza el equilibrio con los puntos A y B a la misma altura. ¿Qué presión absoluta tiene el gas encerrado en el equilibrio? |
 |
|
Bonito ejercicio, estos profes sí que son imaginativos para inventar complicaciones...
Bien, como ya sabés de sobra (y si no lo sabías es hora de que te pongas las pilas) en todo ejercicio de tubos en U la clave es que prestes atención al nivel en el que los líquidos se tocan, o sea al nivel del punto C. |
|
|
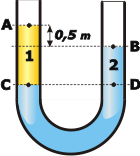
Así queda definido el punto D que no podés dudar que se halla a la misma presión que C (por estar a la misma profundidad en el líquido 2).
Y como los puntos A y B también se hallan a la misma presión (la de la atmósfera), entonces podemos concluir que la diferencia de presión en la columna AC (cuya altura nos pide el enunciado) es igual a la diferencia de presión en la columna BD.
ΔPrAC = ΔPrBD
|
|
|
|
|
Si para cada columna aplicamos el principio general de la hidrostática, tendremos:
ρ1 . g . ΔhAC = ρ2 . g . ΔhBD
Y, como ves, tenemos dos incógnitas, pero hay un dato que todavía no usamos: que la columna del líquido 1 es 0,5 m mayor que la columna del líquido 2...
ΔhAC = ΔhBD + 0,5 m
|
|
uso Pr para presión (lo cual no es del todo correcto) y ρ para densidad |
El resto es aburridísima álgebra: de la segunda ecuación despejo ΔhBD y eso lo meto en la primera. (También cancelo la aceleración de la gravedad).
ΔhBD = ΔhAC — 0,5 m
ρ1 . ΔhAC = ρ2 . (ΔhAC — 0,5 m)
Distribuyo, despejo y calculo:
ρ1 . ΔhAC — ρ2 . ΔhAC = — ρ2 . 0,5 m
ΔhAC ( ρ1 — ρ2) = — ρ2 . 0,5 m
ΔhAC = — ρ2 . 0,5 m / ( ρ1 — ρ2 )
ΔhAC = — 2,6 g/cm³. 0,5 m / — 1,4 g/cm³
|
|
|
|
|
|
Fue dificilísimo, ¿no? Vamos al ítem b). Te darás cuenta que es un nuevo ejercicio, casi independiente del anterior. Hagamos un nuevo esquema que aclare la situación... sabés que en física es casi imposible comunicarse sin una figura. |
|
|
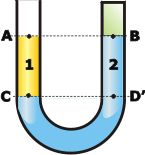
Antes que nada analicemos un poquito esta nueva situación. La columna de la derecha se cerró y atrapó un gas (lo sombreé en verde), ¡que tiene que hallarse a una presión menor que la atmosférica! Eso es obvio, ya que si el punto B ascendió para quedar a la misma altura que A... ¡es como si hubiésemos succionado!, o sea, aplicado una menor presión que lo que había antes, que era una atmósfera.
Otra cuestión obvia es que la columna AC no cambió su longitud y es la misma que calculamos en el ítem anterior, ya que los líquidos son incompresibles. Si no te das cuenta de esas cuestiones estás frito. Además revela que no tuviste infancia y no jugaste con agua, mangueritas y frasquitos como hicieron tus padres, tus abuelos, tus bisabuelos, tus tatarabuelos, etcétera. |
|
|
|
|
El nivel del punto C determina un nuevo punto sobre la rama derecha que llamé D'. Y ahora tenemos:
ΔhAC = ΔhBD'
PrC = PrD'
Aplicando nuevamente el principio general en cada rama...
PrC — PrA = ρ1 . g . ΔhAC
PrD' — PrB = ρ2 . g . ΔhBD'
Y bueno... creo que ya está. Basta con despejar la presión en B que es la de nuestro gas enrarecido...
PrC = PrA + ρ1 . g . ΔhAC
PrD' = PrB + ρ2 . g . ΔhBD'
Igualamos los segundos miembros (recordá que ahora las alturas son iguales):
PrB + ρ2 . g . ΔhAC = PrA + ρ1 . g . ΔhAC
Y despejamos PrB
PrB = PrA + g . ΔhAC ( ρ1 — ρ2 )
Como no se cancelan, la unidades de las densidades habrá que expresarlas en unidades internacionales:
PrB = 101325 Pa + 10 m/s² . 0,93 m . ( —1400 kg/m³)
|
|
|
|
|
|
| Como ves, es menor que la presión atmosférica. Cualquier número mayor que la presión atmosférica resutaría inadmisible. |
|
|
|
|
|
| *Ejercicio que perteneció al segundo examen parcial tomado en noviembre de 2018. |
|
|
|
DESAFÍO: ¿Cuál sería tu conclusión si al encerrar un gas en la rama derecha la diferencia de alturas fuera mayor que los 0,5 metros iniciales? |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización nov-18. Buenos Aires, Argentina. |
|
|
| | |
|
|

