NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
FLUIDOS - PRINCIPIO DE ARQUÍMEDES |
|

|
| |
NMS 16*) Un bloque de aleación liviana de volumen Vb está pegado en una cara de un cubo de madera cuyo volumen es Vm. La relción de volúmenes es Vb = Vm/6. Cuando el cubo se coloca en el agua con el bloque de aleación liviana en la cara inferior, se sumerge hasta 1/3 de la altura del cubo de madera. Si se invierte, quedando el bloque sobre la cara superior, entonces el volumen sumergido del cubo de madera será: |
| |
a) Vm/2 |
b) Vm |
c) Vm/4 |
d) Vm/3 |
e) Vm/8 |
f) 3 Vm/4 |
|
|
No te miento... el enunciado tuve que leerlo tres veces. Pero no pongas cara de sorpresa: vos también sabés que la redacción no es el fuerte de los físicos.
Acá tenés un esquema de la situación inicial: |
|
|
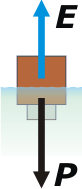 |
Lo que dice Newton es que si el cuerpo está flotando entonces las fuerzas que actúan sobre él deben sumar cero. El empuje que hace el agua, E, y tira para arriba. Y el peso del conjunto (peso del bloque más peso del cubo), P, que tira para abajo.
P = E [1]
Además, según Arquímedes, el empuje es igual al peso del líquido desalojado:
E = Plíq [2]
El peso del líquido (agua) es igual al peso específico del agua por el volumen de agua desalojado, o sea un tercio del volumen del cubo de madera más el volumen del bloque. |
|
|
|
Plíq = γlíq (Vb + Vm/3) [3]
Donde γlíq es el peso específico del líquido. Veamos qué ocurre en el segundo momento, cuando se invierte el conjunto. |
|
|
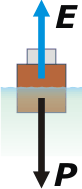 |
Las fuerzas que actúan son las mismas que antes ¡y valen lo mismo! Ya que el peso del conjunto no cambia por estar derecho o cabeza abajo. Newton repite:
P = E [4]
Además, según Arquímedes, el empuje es igual al peso del líquido desalojado:
E = P'líq [5]
El peso del líquido (agua) es igual al peso específico del agua por el volumen de agua desalojado. |
|
|
|
P'líq = γlíq V'm [6]
Donde Vm' es el volumen del líquido desalojado en esta segunda instancia. Pero si mirás bien las seis ecuaciones llegás a la conclusión de que los volúmenes desalojados en ambas situaciones son iguales.
ρlíq V'm = γlíq (Vb + Vm/3)
V'm = Vb + Vm/3 [7]
Pero además, había una relación entre el volumen del cubo y el volumen del bloque, ¿te acordás? (Vb = Vm/6). Entonces:
V'm = Vm/6 + Vm/3
|
|
|
|
|
|
| Al final el ejercicio no era más que una relación entre volúmenes. Hay quien se da cuenta de esto de entrada... y yo podría haber dado la argumentación verbalmente y resolver sólo la cuestión de los volúmenes. Pero ya sabés cómo es (de hinchaquinotos) No me salen. |
|
|
*Este ejercicio fue tomado en el examen final de Física de julio de 2011.
Para ver el tema de examen completo hacer click acá. |
|
|
|
| DESAFÍO: ¿En que cambia el ejercicio si el nivel de agua asciende 35 centímetros? |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente legítima, o sea, este sitio. Última actualización
nov-13. Buenos Aires, Argentina. |
|
|
| | |
|
|

