NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
FLUIDOS - PRINCIPIO DE ARQUÍMEDES |
|

|
| |
NMS 15) Hallar la densidad de la kriptonita verde, sabiendo que para sostener un trozo de 2,2 kg dentro del mar de Kryptón hay que realizar una fuerza de 24,31 N.
Datos: gravedad en Kryptón: 13,2 m/s². Densidad del mar de Kryptón 1,12 kg/L. |
|
El planeta Krypton es un planeta más grande que la Tierra con una gravedad mayor, su composición es básicamente hielo y roca. La forma de vida dominante es humanoide, es decir, básicamente iguales a los humanos. Los kryptonianos viven en estructuras semi-subterráneas que los protegen del intenso frío del exterior, y su sociedad está muchos siglos más avanzada que la humana. Dominan el cuarzo y otros cristales minerales a modo de libros, teoría que actualmente se contempla en la Tierra, logrando cristales perfectos que ópticamente contienen millones de datos. Varios de estos cristales fueron traidos por Súperman a la Tierra.
La kryptonita verde es un material rocoso bastante raro. Las primeras caracterizaciones que se hicieron son las recreadas en este ejercicio. |
|
|
 |
Para conocer la densidad de cualquier cuerpo hay que conocer su masa (que es dato en este caso) y su volumen (que no conocemos). Pero podemos usas nuestros superpoderes mentales.
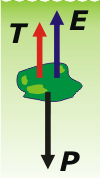
Con la roca sostenida mientras está sumergida en el mar, hay tres fuerzas aplicadas. Veamos si estás de acuerdo: el propio peso de la roca, P; la fuerza con la que se la sostiene, T, que es dato del enunciado y vale 24,31 N; y el empuje que recibe del líquido, E.
Las ecuaciones de equilibrio dirán:
P = E + T [1]
Además, según Arquímedes, el empuje es igual al peso del líquido desalojado:
E = Plíq [2]
|
|
|
|
Y el peso del líquido:
Plíq = γlíq V [3]
Donde V es el volumen de la roca, que como está sumergida totalmente, también es el volumen de líquido desalojado y γ el peso específico del líquido. Además, el peso de la roca es igual a:
P = m . gk [4]
Donde gk es la gravedad en Kryptón, que es dato del enunciado. Arranquemos. Meto la [2] y la [4] en la [1]
m . gk = γlíq . V + T
Recordando la relación entre densidad y peso específico...
m . gk = ρlíq . gk . V + T
De ahí despejamos el volumen...
V = (m . gk — T) / ρlíq . gk
Ahora sí podemos ir a buscar el valor de la densidad de la kriptonita, ρk:
ρk = m / V
ρk = m . ρlíq . gk / (m . gk — T)
ρk = 2,2 kg . 1.120 kg/m³ . 13,2 .m/s² / (2,2 kg . 13,2 .m/s² — 24,31 N) |
|
acordate que peso específico es igual a densidad por gravedad
γ = ρ g |
|
|
|
O, lo que es lo mismo: |
|
|
|
|
|
| No puedo más... estoy muy debilitado... |
|
|
| DESAFÍO: ¿Cuánto vale el volumen del trozo de kriptonita? ¿Cuánto vale el peso del trozo en Kryptón y en la Tierra? |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente legítima, o sea, este sitio. Última actualización
sep-13. Buenos Aires, Argentina. |
|
|
| |
|
|
|

