 |
NO ME SALEN
(PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC)
FLUIDOS
|
|

|
| |
NMS 4* - Se dispone de un tubo en U de ramas iguales y lleno de mercurio hasta 50 cm de los bordes. La presión atmosférica es de 75,5 cmHg. Se obturan ambas bocas y en una de ellas se conecta una bomba de vacío. ¿Hasta qué altura subirá la columna de mercurio en la rama en la que se hizo vacío? (Suponga que no hubo cambios de temperatura). |
|
Uy, que ejercicio más bonito. Vamos a resolverlo reparando qué ocurre en cada etapa del proceso que cuenta el enunciado. Siempre nos ahorra mucho esfuerzo el contar con buenos esquemitas. |
|
|
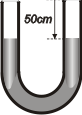
Repasemos, el enunciado, a ver si estás de acuerdo: las dos ramas abiertas al aire... eso implica que en ambas superficies tenemos la misma presión (es un día de baja presión, aunque no mucho) por lo tanto tienen que hallarse al mismo nivel.
El nivel en ambas ramas está 50 cm por debajo de las bocas abiertas del tubo. Hasta acá, nada difícil. |
|
|
|
cuando los tubos están abiertos al aire, los niveles en ambas ramas son iguales |
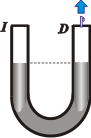
Ahora sellamos ambas bocas, con lo cual encerramos un poco de aire en cada una, que conserva la presión que tenía antes del cierre, o sea: 75,5 cmHg.
Pero en una de las ramas -digamos, la derecha- se coloca una bomba de vacío con la idea de extraer todo el aire que había quedado encerrado en ese sector superior de la rama derecha. |
|
|
|
si las ramas del tubo tienen el mismo grosor constante, todo lo que el líquido ascienda por una rama, descenderá por la otra |
| Existe un error intuitivo en este fenómeno. La gente de a pie piensa que el mercurio sube por la rama derecha porque el vacío lo chupa. Sin embargo esto es incorrecto y aberrante. (Pero no te asustes, a todos nos pasó, y no tiene ninguna importancia). |
|
|
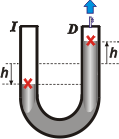
Lo que en realidad ocurre es que el aire que quedó en la rama izquierda empuja al mercurio hacia abajo, y éste cede corriéndose hacia la rama derecha que ahora encuentra desocupada.
¿Hasta dónde sube el mercurio en la rama derecha? Eso es justamente lo que tenemos que averiguar. Pero va a depender exclusivamente de la presión que ejerza el aire que quedó encerrado en la rama izquierda. |
|
|
|
en los espacios sin mercurio (aire o vacío) la presión es constante, y es la presión que empuja al mercurio en sus partes superiores (cruces rojas) |
Uno podría pensar que la presión en esa rama cerrada es la misma que tenía el aire antes de obturar el tubo. Pero no. Porque ese gas ha variado el volumen que ocupaba... y al aumentar el volumen debe haber disminuido la presión que ejerce. La ecuación que describe esa variación es la Ley de Boyle y Mariotte, que dice que en dos momentos, 1 y 2, se cumple esta relación entre volúmenes, V, y presiones, P...
P1 . V1 = P2 . V2
Válida sólo para temperaturas que no cambian (que es lo que ocurre en el ejercicio). Como las ramas son idénticas y de sección, S, constante, puede escribirse así:
P1 . S . h1 = P2 . S . h2
P1 . h1 = P2 . h2
No te distraigas. Estamos hablando exclusivamente de lo que ocurrió en la rama izquierda. Antes del movimiento del mercurio el volumen de aire tenía una presión P1 de 75,5 cmHg y una altura h1 de 50 cm. Luego del movimiento del mercurio la presión, P2, es desconocida y la altura será h2 = ( 50 + h ) cm. Donde h es el número de centímetros que descendió el mercurio en la rama izquierda (y que es la misma altura que ascendió en la derecha). Resumiendo:
75,5 cmHg . 50 cm = P2 . (50 + h) cm
|
|
el volumen de un cilindro, V, es igual al producto de la altura del cilindro, h, por la sección S
V = S . h
para no hacer muy complejas las cuentas vamos a llamar h al número de centímetros que asciende o desciende el mercurio
|
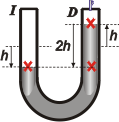
Por otro lado, la nueva presión del aire en la rama izquierda, P2, debe ser igual a la presión que ejerce la columna mercurial en la otra rama hasta el mismo nivel de la superficie en la izquierda. Si esa presión la medimos en centímetros de mercurio vale:
P2 = 2h cmHg
Esto no es otra cosa que el experimento de Torricelli. |
|
|
|
la presión en el borde superior en la rama derecha vale 0
las presiones en las posiciones de igual nivel (cruces rojas de abajo) son idénticas |
Juntemos todo (las unidades se cancelan, fijate):
75,5 . 50 = 2h . (50 + h)
0 = – 75,5 . 50 + 2h . 50 + 2 h²
0 = – 3.775 + 100 h + 2 h²
Con lo que arribamos a una ecuación cuadrática, sencillita, que la resolvemos con la fórmula mágica de los griegos y obtenemos... |
|
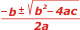
c = – 3.775
b = 100
a = 2 |
|
|
|
| No te vayas de este ejercicio sin verificar que las presiones en cada posición son las correctas. Ni sin resolver el DESAFÍO. |
|
|
|
|
|
| *Ejercicio adaptado de Termodinámica, teoría cinética y termodinámica estadística de Sears - Salinger. Ed Reverté 1978. |
|
|
|
DESAFÍO: Repetir el ejercicio pero suponiendo ahora que la rama en la que se hace vacío tiene un diámetro doble la otra rama. |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-10. Buenos Aires, Argentina. |
|
|
| | |
|
|

