 |
NO ME SALEN
(PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC)
FLUIDOS
HIDROSTÁTICA
|
|

|
| |
| NMS 01* Dos líquidos inmiscibles se encuentran en equilibrio formando capas de igual espesor, como muestra la figura, en un recipiente abierto por arriba y sometido a la presión atmosférica. Las presiones en los puntos A (a mitad de la capa superior) y B (fondo) son: PA= 1,2 atm y PB = 2,6 atm. Si ρA es la densidad del líquido superior, ¿cuánto vale la densidad del líquido inferior? |
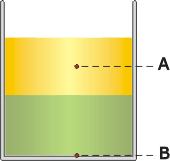 |
|
Este ejercicio tiene esta gracia: es recontra sencillo, hasta se puede resolver mentalmente si tenés una pizca de ingenio (y bastante experiencia y nervios de acero). También tiene la gracia de que guarda una trampa en la manga... yo voy a caer en la trampa adrede para que veas cómo escapo sin un solo rasguño.
Inmiscibles significa que no se mezclan, como el aceite y el vinagre. Y si los vertís suavemente para que no se rompan, el menos denso queda flotando sobre el más denso (el aceite arriba, el vinagre abajo). Pero si los vertís arriba de la ensalada es mejor.
Acá te repetí el esquema del ejercicio pero, para que me puedas seguir los razonamientos, agregué dos puntos más: uno ubicado en la superficie libre, S, y otro en la interfase de los dos líquidos, M. |
|
|
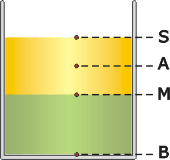 |
Si en la superficie, en el punto S, la presión vale cero, entonces en el punto M la presión tiene que valer el doble de lo que vale en A. Esto surge de aplicar el principio general de la hidrostática que dice que profundidad y presión son directamente proporcionales (Δp = ρ g Δy). De modo que si al bajar desde A hasta M se duplica la profundidad (acordate que A estaba en el medio justo del líquido de arriba), también debe duplicarse la presión.
Por lo tanto la presión del punto M debe ser...
pM = 2,4 atm
|
|
|
|
Ahora, como la presión en el fondo vale PB = 2,6 atm significa que desde M hasta B la presión aumenta 0,2 atm...
ΔpMB = 0,2 atm = ρB g Δy
Mientras que en el líquido de arriba...
ΔPSM = 2,4 atm = ρA g Δy
como la diferencia de profundidad (y la gravedad) es la misma para ambos líquidos, un modo sencillo de relacionar las dos ecuaciones es dividirlas miembro a miembro (así, la diferencia de profundidad y la gravedad se cancelan).
0,2 atm / 2,4 atm = ρB / ρA
De donde
ρB = ρA / 12
¡Imposible! Eso nos está diciendo que la densidad del líquido superior es mayor que la del líquido inferior. ¡Arquímedes estaría revolviéndose de horror en su tumba! ¿Habrá algún error? ¿Habrá alguna trampa? Llamalo como quieras... pero nada indicaba de antemano que las presiones de las que hablaba el enunciado fueran presiones manométricas (de la escala relativa). Seguramente se trata de presiones dadas en escala barométrica (absoluta). De modo que la presión en la superficie del líquido superior no vale cero sino 1 atm. Rehagamos la historia, entonces.
PS = 1 atm
PA = 1,2 atm
ΔPSA = 0,2 atm
ΔPAM = 0,2 atm
ΔPSM = 0,4 atm = ρA g Δy
PM = 1,4 atm
ΔPMB = 1,2 atm = ρB g Δy
Volvemos a hacer la misma división de antes, pero ahora fijate lo que da...
1,2 atm / 0,4 atm = ρB / ρA
|
|
 |
|
ρB = 3 ρA |
Y sin un rasguño... |
|
|
|
Moraleja: nunca te conformes con arribar a un resultado y te quedes sin discutirlo, sin interpretarlo. Es preferible que escribas un cartelón diciendo que no aceptás el resultado porque es físicamente imposible por tal o cual razón, a que lo dejes sin decir nada. Te lo cobran con intereses. |
|
|
*Este ejercicio perteneció al primer parcial de Biofísica tomado el 6 de oct. de 2006. |
|
 |
| |
|
DESAFÍO: Sólo para hacer mentalmente: ¿cuánto vale la presión en el punto medio del líquido inferior? |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Quien no cite la fuente será penado con reclusión en la Antártida y trabajos forzados. Última actualización sep-08. Buenos Aires, Argentina. |
|
|
| | |
|
|

