home  | más de hidrostática | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
   NO ME SALEN
   (PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC)
   FLUIDOS
   HIDROSTÁTICA		  

desesperado

15- Dos líquidos inmiscibles se encuentran en
equilibrio, uno sobre el otro, formando capas de
igual espesor de 1 m cada una, en un recipiente
abierto por arriba y sometido a la presión atmosférica
(patm = 100 kPa). Las densidades de los
líquidos son δ1 = 0,8 g/cm3 y δ2 = 1 g/cm3:
    a) Calcule la presión absoluta en el fondo del recipiente.
    b) ¿Cuántos centímetros hay que descender, respecto de la superficie libre del líquido superior en contacto con la atmósfera, para registrar una presión absoluta de 111 kPa?
    c) Realice un gráfico de la presión manométrica en función de la profundidad desde la superficie libre del sistema hasta el fondo del recipiente, indicando los valores significativos que considere necesarios para la correcta descripción de la variación de la presión.		    

Este es un clásico, aparece en 9 de cada 5 exámenes. Y una de las claves para la resoución exitosa es que aciertes el orden en que se colocan los líquidos inmiscibles, o sea, que no se mezclan entre sí y forman capas horizontales. A esta altura del partido supongo que ya lo tenés incorporado en tus reflejos: los cuerpos de menor densidad quedan arriba y el de mayor densidad se va al fondo. En nuestro caso el líquido 1 es el de arriba.

    a) Calcule la presión absoluta en el fondo del recipiente. Justo para esta pregunta obtenés el mismo resultado si te ubieras equivocado en la disquisición anterior. Resolvamos.

    
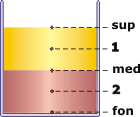
Fluídos - Ricardo Cabrera  

Ahí tenés el esquemita en el que aproveché para ponerle nombre a los puntos, las posiciones, que van a ser necesarios mencionar.

La variación de presión entre el punto superior, sup, y el punto medio, med, nos lo indica el principio general de la hidrostática:
   

Δprsup-med = δ1 . g . h1

prmed — prsup = δ1 . g . h1

prmed = prsup + δ1 . g . h1

prmed = 100.000 Pa + 800 g/m3 . 10 m/s² . 1 m

prmed = 108.000 Pa

Ahora hacemos lo mismo en la capa de abajo, entre el medio y el fondo, fon:

Δprmed-fon = δ2 . g . h2

prfon = 108.000 Pa + 1.000 g/m3 . 10 m/s² . 1 m

  


        

 prfon = 118.000 Pa  
   

    b) ¿Cuántos centímetros hay que descender, respecto de la superficie libre del líquido superior en contacto con la atmósfera, para registrar una presión absoluta de 111 kPa? Es obvio que podemos encontrar esa presión dentro del líquido de abajo... entonces arrancamos de 108 kPa y vamos para abajo.

111.000 Pa — 108.000 Pa = δ2 . g . hb

3.000 Pa = 1.000 g/m3 . 10 m/s² . hb

hb = 0,3 m

La pregunta pide medirlo desde la superficie libre arriba de todo, entonces:

  

        

 descenso = 130 cm  
 
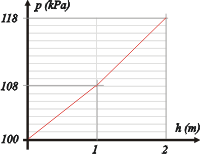
Vamos con el gráfico.  
Fluídos - Ricardo Cabrera  

Una de las cuestiones más importantes al interpretar este tipo de gráficos es recordar que la presión aumenta con la profundidad. Tal vez mi elección de la letra h para indicar profundidad no sea la más feliz (porque h se asocia con altura). Tal vez Δy sea mucho mejor, no sé. Pero lo dejé a propósito para poder advertirte sobre ésto: es una de las fuentes más común de errores en la interpretación de estos gráficos.
 
 

 

 
PARA SABER MÁS: Acá tenés la teoría y resolución de los tubos en U. Fluídos - Ricardo Cabrera
 
 
   
Algunos derechos reservados. Se permite su reproducción citando la fuente. La Asociación Internacional de Físicos Constructivistas y el Club Boca Juniors recomiendan NO utilizar este material didáctico por considerarlo altamente pernicioso. Última actualización mar-20. Buenos Aires, Argentina.